I have this PID originally on my HLT and BK but now it is relegated to monitoring my MT. The Inkbird instructions suck. I recall having to watch a video to get some settings at least somewhat close and I think it was probably the Doug on Youtube video you mentioned. If I recall correctly, it involved setting the P, I, D values on the Inkbird? I was completely clueless regarding how these worked at the time and I set the values to those I saw in the video. Those won't work in all likelihood for you because the video was heating water/beer. You are heating air, which heats much more rapidly than water. If you know this, my apologies, but the PID stands for Proportional, Integral, and Derivative, all mathematical terms. Some time ago I read up on this but it's faded a bit so I am going to cheat and use a little AI below.
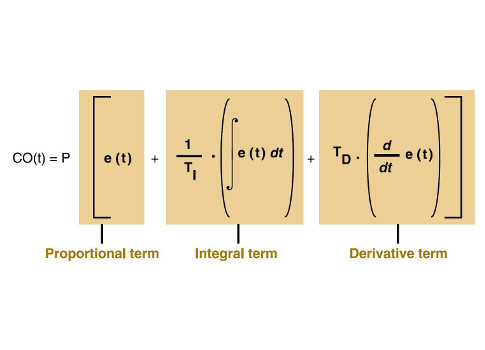
Doug sounds like he's zeroed in on possible issues and in plainer (more coherent than me) language. He's provided a potential physical possibility with the probe response and then the issue of rapid overshoot. I'm just expanding a bit on the settings since the manual for this model is awful. Sounds like maybe P is set too high? And also some adjustment of D maybe is needed? But all Inkbird says is that those values range from 0-9999 and the I & D are based on seconds. I grabbed the equation below just to show how the equation looks and mainly just to show that the component terms aren't simple. Picking say 5000 for I or D probably won't be half the effect of picking 9999. Maybe for P, but I never experimented with changing these parameters.
I learned a lot more about how my Inkbird was working by reading one of the Auber Instrument manuals for a similarly configured model. Sorry though I don't remember the exact model but the instructions discussed many of the same settings available on the Inkbird.
I am not sure if the autotune (selftune) changes the values of P, I, and D that you set or if it stores them in a different spot. You could check that by running a selftune and examining those values afterwards.
And that's about all I know to help, all the following is AI derived. It tracks correctly as much as I remember reading on the topic.
The proportional term in a PID controller calculates a correction that's directly proportional to the current error between the desired setpoint and the system's output. This term is responsible for the initial "push" that helps the system move towards the setpoint. The larger the error, the larger the proportional correction, and the faster the system will respond.
Here's a more detailed breakdown:
- Purpose:
The proportional term aims to minimize the error between the setpoint and the system's output as quickly as possible.
- Mechanism:
It calculates a correction based on the current error by multiplying the error by a proportional gain (Kp).
- Effect:
Increasing Kp makes the system respond faster, but can lead to overshoot. Overshoot occurs when the system moves past the setpoint before settling down.
- Relationship to other terms:
The proportional term works in conjunction with the integral and derivative terms to provide a more robust and accurate control response. The integral term helps eliminate steady-state errors, while the derivative term helps dampen oscillations and prevent overshoot.
In a PID controller, the integral term, denoted by "I", helps eliminate steady-state error and fine-tunes the system over time. It does this by calculating the sum of all past errors and adding it to the control output. This accumulated error signal ensures that the system converges to the desired setpoint, even with
constant loads or disturbances.
Here's a more detailed explanation:
1. Eliminating Steady-State Error:
- A proportional (P) controller alone may produce a steady-state error, meaning the output stays slightly off the desired setpoint even after settling.
- The integral term addresses this by considering the history of errors and gradually adjusting the control output to minimize this difference.
2. Accumulating Error over Time:
- The integral term calculates the integral of the error over time, effectively summing up all past errors.
- This accumulated error signal is then used to modify the control output, ensuring a more accurate response over time.
3. Fine-Tuning and Stability:
- By taking into account the cumulative error, the integral term helps to refine the system's behavior and improve its stability.
In essence, the integral term in a PID controller acts as a "long-term memory" of the error, allowing the system to adjust and converge to the desired setpoint more precisely over time.
AI Overview
Learn more
In a PID controller, the derivative (D) term anticipates future errors by considering the rate of change of the error. It helps reduce overshoot and improve stability, especially in systems with rapid changes, by essentially acting as a "dampener" on the control effort.
Here's a more detailed explanation:
- Predicting Future Errors:
The D term looks at how quickly the error is changing and uses that information to predict where the process variable is likely to be in the near future.
- Dampening Effect:
By anticipating the change, the D term can adjust the control output to counter the potential overshoot or oscillation. This helps the system settle more quickly and stably at the desired setpoint.
- Improving Stability:
The D term can improve the stability of a PID controller by reducing oscillations and preventing excessive overshoot, particularly when dealing with systems that are prone to rapid changes.
- Amplifying Noise:
It's important to note that the D term can also amplify measurement noise, which is a common consideration in PID tuning, according to Control Station.


























![Craft A Brew - Safale S-04 Dry Yeast - Fermentis - English Ale Dry Yeast - For English and American Ales and Hard Apple Ciders - Ingredients for Home Brewing - Beer Making Supplies - [1 Pack]](https://m.media-amazon.com/images/I/41fVGNh6JfL._SL500_.jpg)































