Bru'n Water does not use DI pH in its calculations. It uses a malt acidity in combination with the alkalinity of the brewing liquor to arrive at a net acidity that is then correlated to a predicted mash pH.
How does one determine "malt acidity"? IOW if I have a sample of malt on the bench, how do I measure this.
I can't see how a DI pH value can reliably be used in the complexly buffered mash system, thus the reason I never considered DI pH in practice.
You really need to understand this because it is apparent from your comments that you don't appreciate that what you are advocating as an alternative, i.e. modeling malt titratable acidity, is exactly what we are doing here except that we are basing our model on measurement, to the extent possible, rather than some empirical relationship between the malt type or color and the characteristics of the curve.
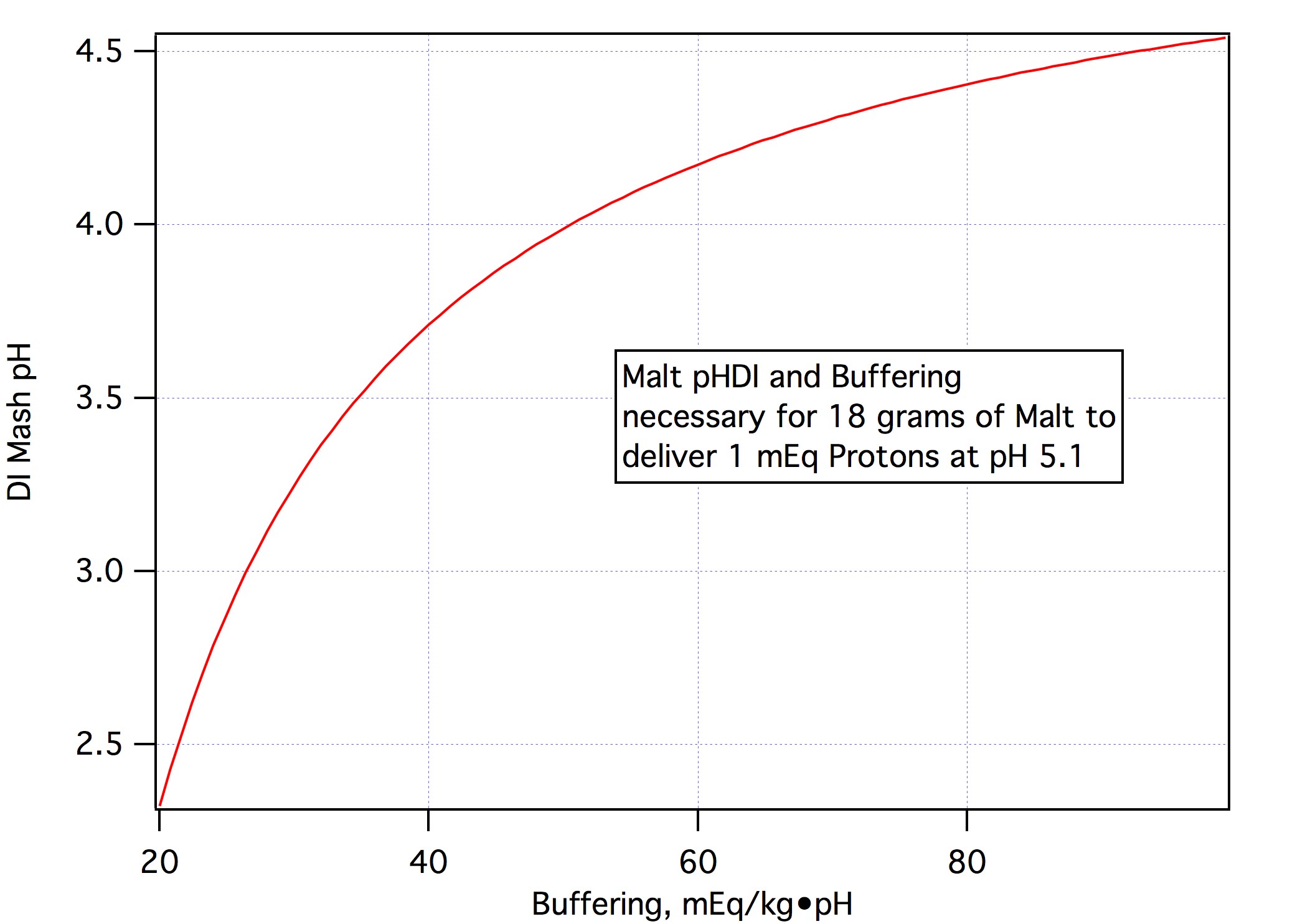
It is obvious that while best results (and these can be really good) require that we determine the actual titration curve for each malt which requires multiple pH measurements we can get a pretty good estimate of the "curve" from a single measurement by assuming that it is linear and that we know its slope to be 45.7 mEq/kg•pH. That single measurement is, of course, the malt's DI mash pH. Malts' titration curves don't all have slope 45.7 and they aren't linear so one can, of course, do better by taking at least one other measurement to determine what the slope actually is (this is the approach Kai originally took and is, I believe, the basis for Brewer's Friend) and better still enough additional measurements to determine the parameters a, b, and c which reproduce the titration cuve in the form:
mEq/kg = a*(pHz - pHdi) + b*(pHz - pHDI)^2 + c*(pHz - pHDI)^3
pHz is the pH realized when mEq/kg acid has been added to a kg of the malt in question. When using the titration curve to control or predict mash pH pHz represents the target pH. It depends much more strongly on pHDI than on any of the other parameters as you can easily see by calculating the total differential WRT to each:
∆mEq/kg = -∆pHdi*(a + 2*b*(pHz - pHDI) + 3*c*(pHz - pHDI)^2)
+∆a*(pHz - pHdi) + (pHz - pHDI)^2*∆b + (pHz - pHDI)^2
To give a general idea we observe that a is about -45 mEq/kg•pH for most malts (excepting sauermalz) and that most malts are fairly linear so that b and c tend to be small relative to a and that, for base malts pH - pHdi tends to be 0.4 pH or less for most values. For Crisp's Maris Otter the parameters are (a = -46.589, b= 6.3516 , c = -2.623, pHdi = 5.69). The grain related error in pH from mis modeling of the mEq/kg calculation is simply the error in mEq/kg divided by the buffering of the mash which is, for each grain approximately a so we can say that, approximately,
∆pH ≈ -∆pHdi -∆pHdi*(2*(b/a)*(pHz - pHDI) + 3*(c/a)*(pHz - pHDI)^2)
+(∆a/a)*(pHz - pHdi) +(∆b/a)* (pHz - pHDI)^2*) + (∆c/a)*(pHz - pHDI)^3
Putting in the numbers for Crisp MO
∆pH ≈ -∆pHdi + ∆pHdi*(0.078 + 0.014)
-(.29/a)*∆a+ (0.1682/a)*∆b -(0.073/a)*∆c
At this point we would model the errors as random variable and look at the rms error
s_pHrms = sqrt( (1.092*s_pHd)^2 + (s_a*0.0124493)^2 + (s_b*0.168)^2 + (s_c*0.073)^2 )
s_x in this last formula represents the standard error in an estimate.
If we know the titration curve shape perfectly (s_a = s_b = s_c = 0) then the error in our pH approximation will be approximately 1.09 times our error in knowledge of the DI mash pH. This is why it is so important that we know that. If we have perfect DI mash pH knowledge (s_pHDI = 0) but our estimate of the slope is in error (rms) by 14 mEq/kg•ph (the standard deviation of all the malt slope data I have excluding sauermalt's) and we assume the curve is linear (which this malt isn't) then the standard error in the pH would be 0.09 pH. Actual mash pH's would differ from this and the analysis would be based on weighted sums of malt masses but the message should be clear: If we have the malt's DI pH we can get by with a pretty good size error in knowledge of slope. But, of course, if we know the slope we can knock out the slope part of the error budget. And if we know the curvature we can knock those errors out too. Then you have a robust method.
The argument that pH can't relate what is in a wine like a titratable acidity test can, is the reasoning behind going with the malt acidity approach in Bru'n Water.
You seem to be missing the essential point that titratable acidity is a function of pH. The DI mash pH is simply the point on the titration curve at which no acid or base has been added.
Its a strong reason why its model seems to be more robust than others.
It may be more robust than some but it is certainly less robust than a model that takes in pHDI as an input. If you are using an acidity model you
must have a titration curve and, as you are not iterating for an answer (AFAIK) your "curve" must be linear. That "curve" requires two parameters to describe it: slope and the value of pH at some level of added base or acid. It doesn't mater what level is chosen/ The obvious one is 0 and the pH at that point is the DI pH. Whether you realize it or not you are effectively doing what I am describing here but as you must deduce pHDI
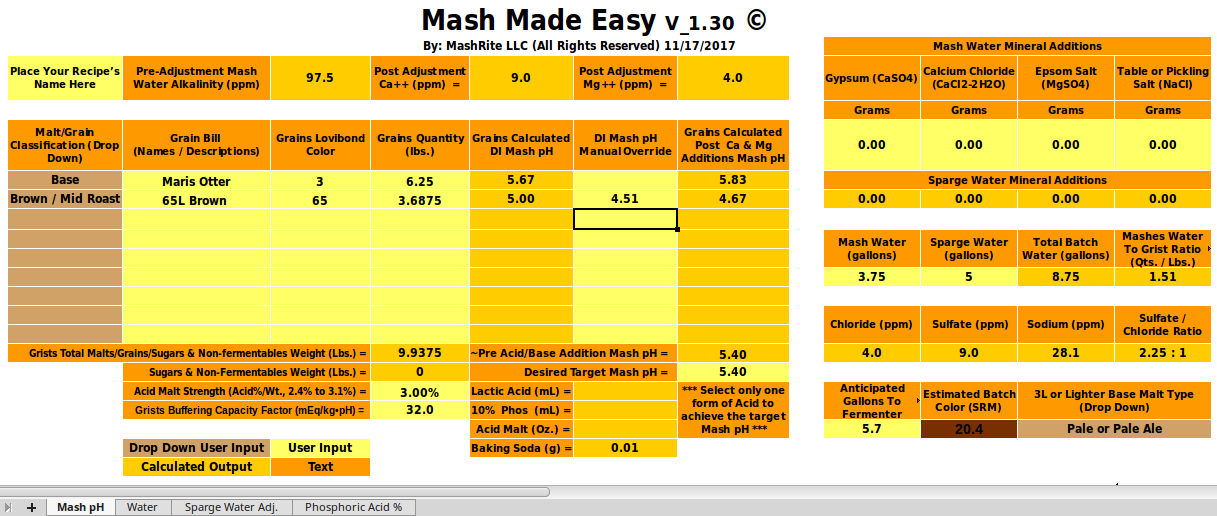
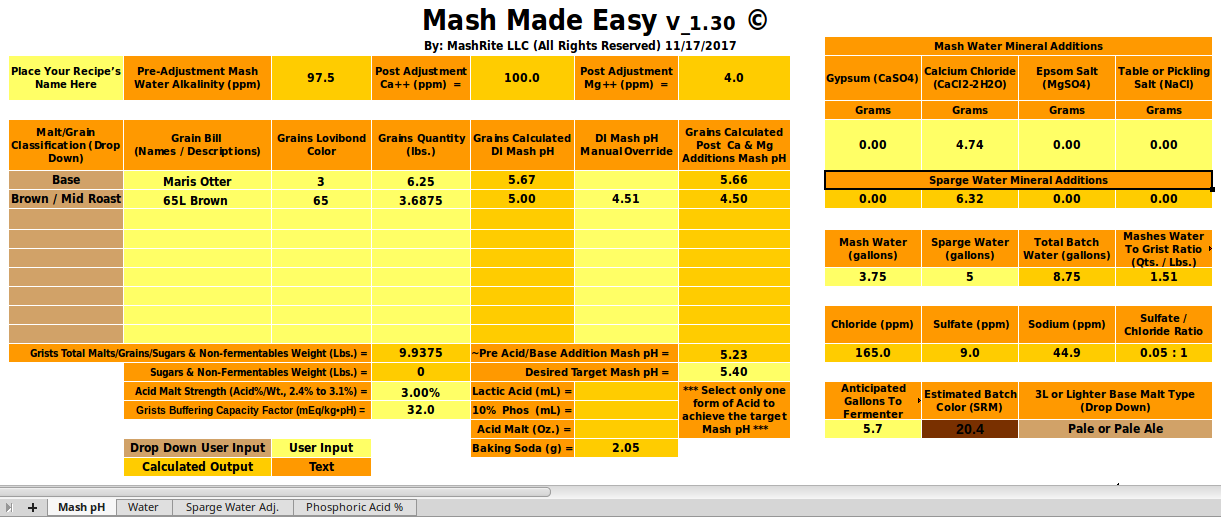
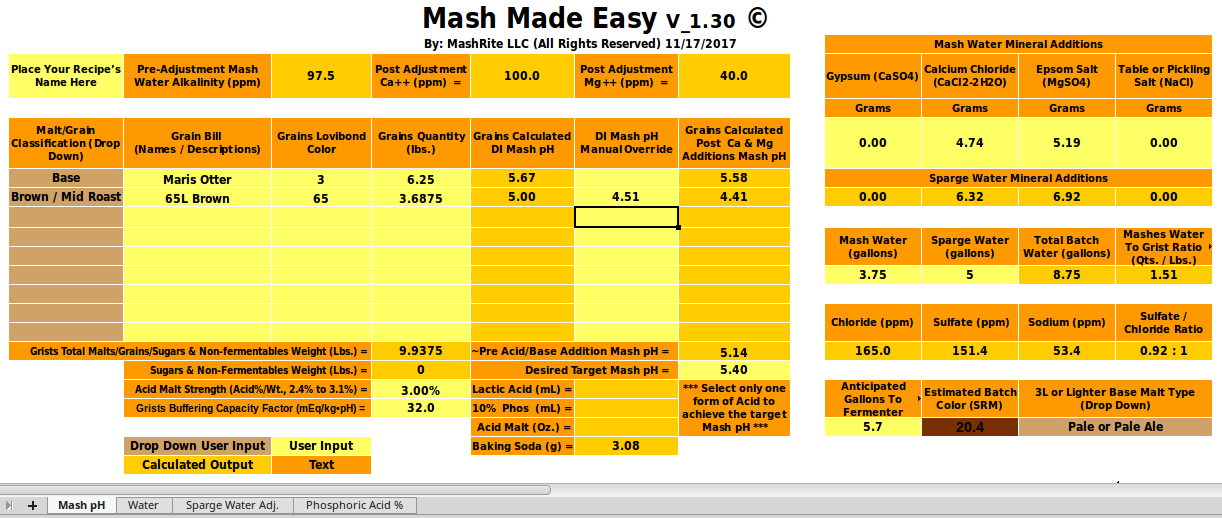
and slope (a) from the malts' descriptions and/or colors you clearly can't get estimates of mash pH that are as good as a program that actually knows the DI pH (unless it makes really bad slope estimates. In the case in point here OP has measured the pHDI of his malt and we can, using that in a robust program, get a much more reasonable estimate of mash pH (about 5.6) than he was getting from Bru'n Water.
You'll never see a vintner considering pH over TA when assessing the quality and character of their products.
And you'll see precious few brewers measuring the titratable acidity of his beer. Well, lambic brewers probably do like to see TA data. But this is kind of a non sequitur as we are talking about mash pH prediction, not QA.
Just to make it abundantly clear
1)You are using malt acidity
2)Kai is using malt acidity
3)Silver is using malty acidity
4)A.J. is using malt acidity.
The latter two are just doing it more robustly by using measurement data when they can get it.

































![Craft A Brew - Safale BE-256 Yeast - Fermentis - Belgian Ale Dry Yeast - For Belgian & Strong Ales - Ingredients for Home Brewing - Beer Making Supplies - [3 Pack]](https://m.media-amazon.com/images/I/51bcKEwQmWL._SL500_.jpg)