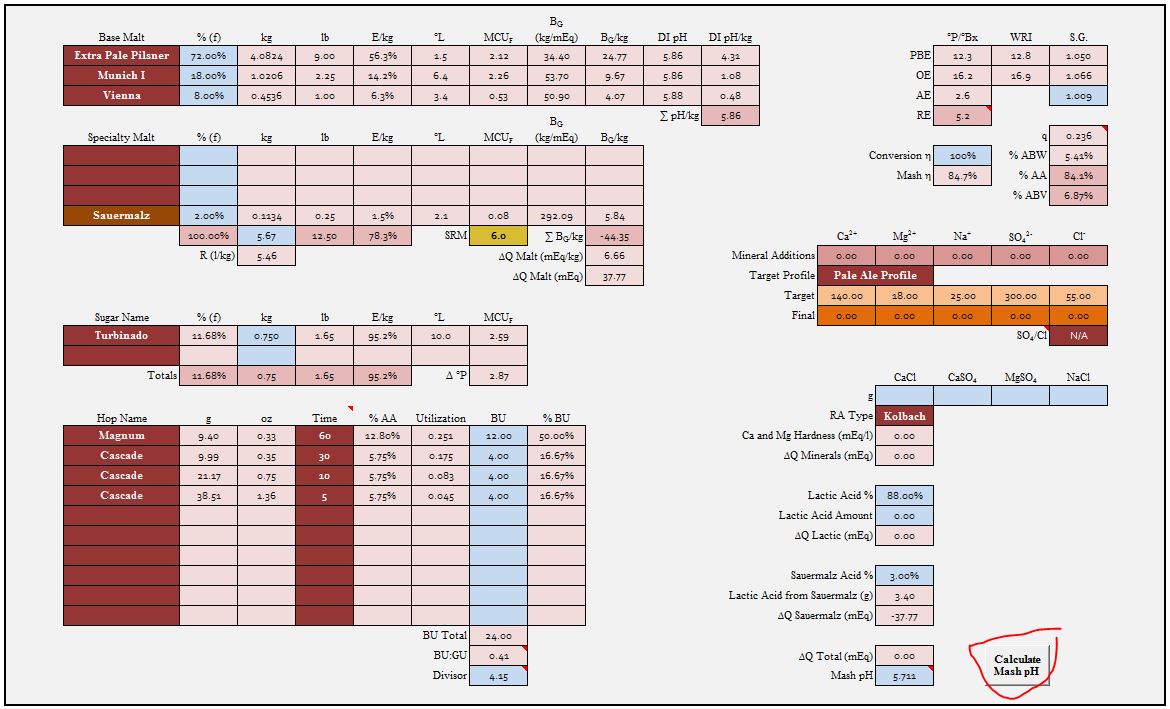
Why limit yourself to the linear form? The cubic form does not preclude the use of the linear malt model in cases where you only have sufficient data to model a malt with two terms (i.e. models derived from colors or Kai's measuremnt). Plus you get the advantages of the more robust treatment of alkalinity.
But I really wanted to talk about the Solver. I think it's great. I love it. I always say that if you think you are using Excel but aren't using the Solver then you aren't really using Excel. BUT - when I told John Palmer that he most certainly should include it in his book (I came up with the charge method while helping him with the mash pH estimation part of it) he said he didn't want to get into something radically new and when I first presented the charge method at an MBAA conference and asked how many people in a room used Excel over half (15? guys) said they did but only 3 said they used the Solver (and one was Karl Siebert - college professors don't count). IOW people don't like the Solver or don't know about it or are afraid of it. And you have to admit it's clumsy to use. You have to set up the problem each time you want to solve it. For guys like us in the thick of the problem that's OK and its a wonderful tool that can help us develop programs for the Suds-Water-Works-Good types but I don't think that you are going to get those guys to use Solver. They want to put in malt type, bicarbonate and acid amounts and have the pHz estimate pop up automatically. Now perhaps you can set up a macro to invoke Solver (never thought of that before but why not?) but there is another approach. The spreadsheet below, based on the Voltmeter spreadsheet we've been fiddling with here does go directly to pHz estimate without using Solver.
View attachment 579048
View attachment 579049
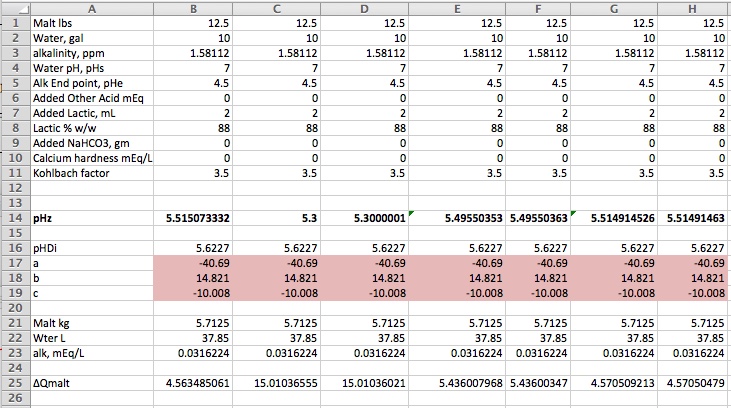
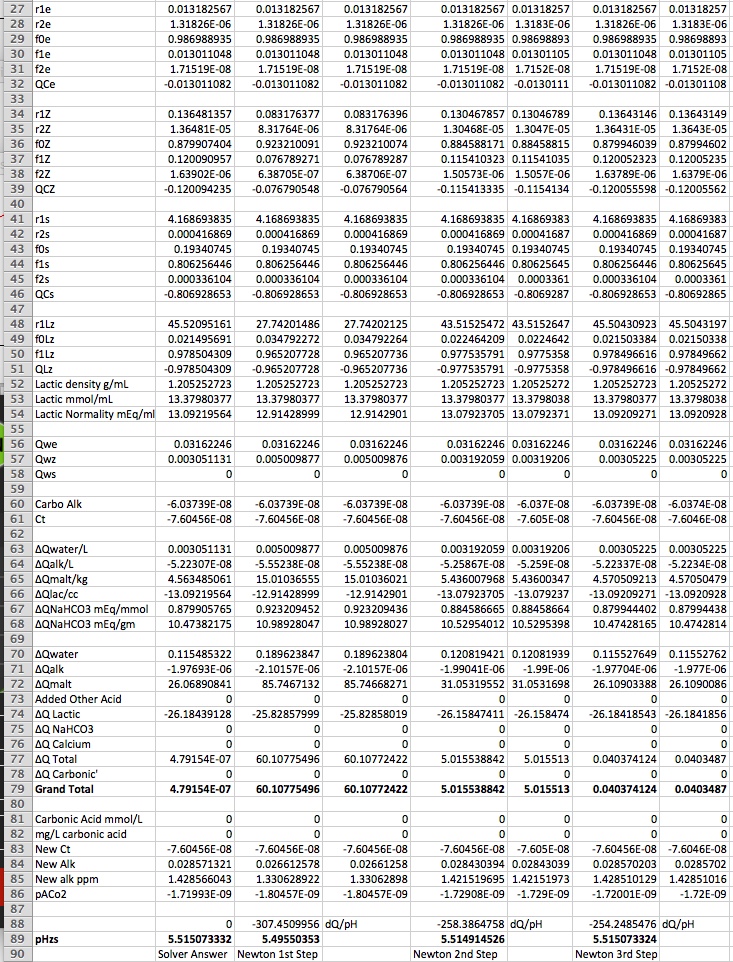
Column B is used to find the pH that would be realized when 2 mL of 88% lactic acid is added to 10 gal of DI water and used to mash 12.5 lbs of Weyermanns Pils. The answer, using the Solver, is pHz = 5.515 (to 3 decimal places). Look at row 89. The answer is copied in B89. In column C we suppose we don't know about the Solver and guess that pHz = 5.3. Looking at C79 we see that the total Q change is 60.1 and thus realize that 5.3 isn't a very good guess. So in Column D we add 0.0000001 to the pH and compute the new charge change sum. It isn't very different from the charge obtained with 5.3 exactly but the ratio (∑∆Q(5.3000001) - ∑∆Q(5.3))/0.0000001 (computed in cell B88) tells us how much change a unit pH change causes in ∑∆Q and we know that if we have 60.1 mEq too much charge at pH 5.3 we ought to try a pH higher by that charge divided by dQ/dPH. This is in Cell C89. Compare this to B89. Pretty close but not quite on. Those who stayed awake in their high school math classe will recognize the genius of Sir Isaac at work here and so we have labeled C89 Newton 1st Step.
In column E we try again with our new estimate of 5.49550353 and find ∑∆Q = 5.01. Still not 0 but closer to 0. Again we find dQ/dpH and note that it is now 258 vs 307 mEq/pH. These numbers are, of course, the buffering of the mash at, respectively, pH 5.3 and 5.495. So much for those who think this problem is linear! Proceeding as above we get a new estimate of pHz = 5.5149. Close enough to 5.5151 to satisfy most but as we are quark chasers we take one more step to get ∑∆Q down to 0.04 and a pH estimate identical to the Solver solution down to the 7th decimal place.
Were someone to use Newton's method in a practical spreadheet he would, of course, hide all these extra columns on a back page or make them invisible on a main page. And, of course, if he wanted to be able to solve for the amount of lactic acid for a given pH he'd have to figure out some logic for that.












































![Craft A Brew - Safale BE-256 Yeast - Fermentis - Belgian Ale Dry Yeast - For Belgian & Strong Ales - Ingredients for Home Brewing - Beer Making Supplies - [3 Pack]](https://m.media-amazon.com/images/I/51bcKEwQmWL._SL500_.jpg)