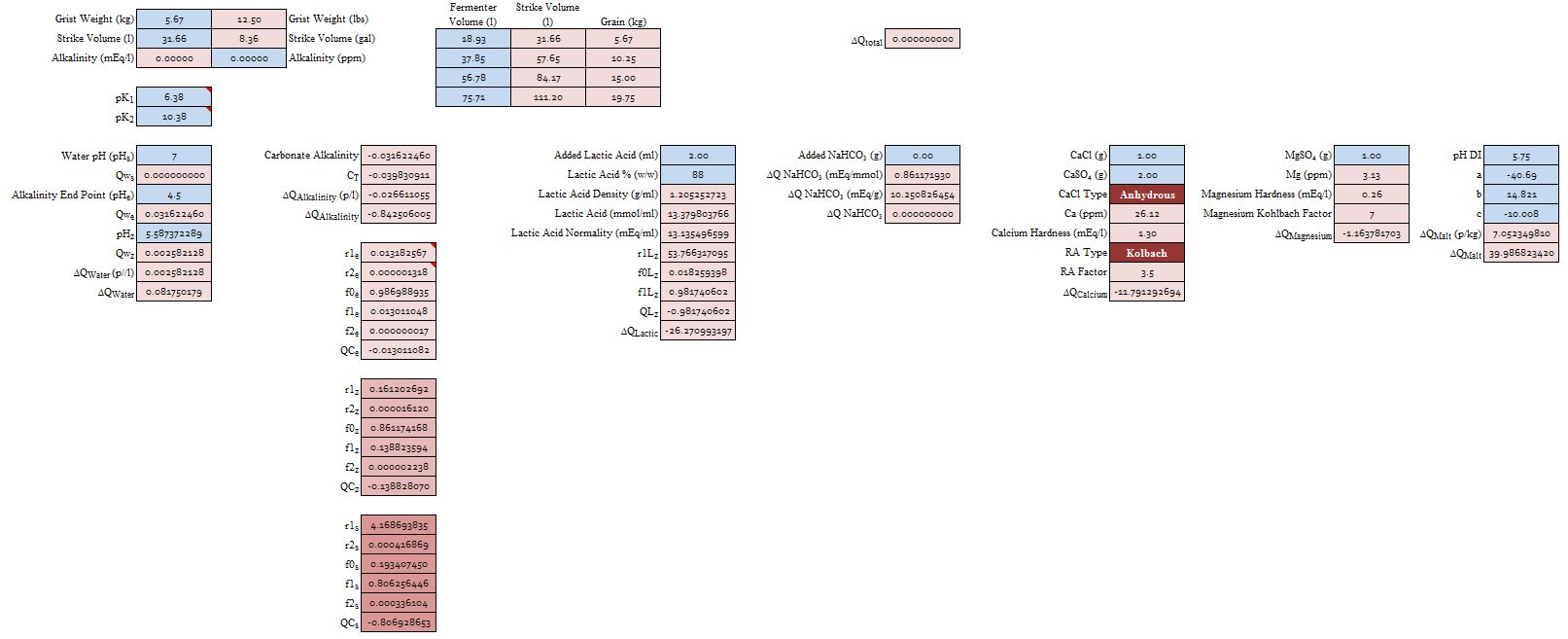
I've noted in some posts here that in some of the spread sheets RA is used to estimate mash pH or mash pH shift, Martin has stated plainly that he uses RA and, though I tried to convince him otherwise, John Palmer thinks RA is the way to go to the point where he told me he wanted to make it the central theme of his book. So I thought I'd see if RA really has a place here. From a purely empirical point of view of course it does. If we have water with bicarbonate in it (alkaline water) and add a bunch of calcium and malt we know that the calcium will react with the phytin to produce acid which, clearly, will neutralize some of the bicarbonate thus reducing the effective alkalinity. The alkalinity not removed by the H+ ions from this reaction is 'residual'. It was Kolbach's intent to present a measure which could be used to compare source waters. Roughly speaking, a water with twice the residual alkalinity of another water would require twice the acid
to treat the water as would be required to treat the other water.
As stated several times throughout the thread in order to predict mash pH or determine the amount of acid (or base) required to set a desired mash pH we must solve
-∑_i Vi*ci*Qai(pHz) + ∑_i (mi/gi)*Qbi(pHz) + Vw*Ct*(Qc(pHz) - Qc(pHs)) + Vw*(Qw(pHz) - Qw(pHs) + Vw*H/3.5 + ∑_i mi*(ai*(pHz - pHDi) + bi*(pHz - pHDi)^2+ci*(pHz - pHDi)^3) = 0
for either pHz or one of the acid (Vj representing the volume of an acid of molar strength gi) or base terms (mj representing the mass of a solid base with molecular weight gi) depending on whether we are estimating or setting pHz. Ct is the total carbo per liter of mash water (volume Vw), pHs is that water's pH, mi are the masses of the individual malts, ai, bu and ci are their coefficients and pHDi their DI mash pH's. Now this equation does not contain RA but it contains something like it. Kolbach defined RA as simply
RA = alk - ([Ca++]/3.5 + [Mg++]/7) in which alk is the water's alkalinity (in mEq/L) and the bracketed quantities the hardnesses in mEq/L. To simplify
RA = alk -H/3.5 in which H = [Ca++] + [Mg++]/2
Though Kolbach probably never intended it most spreadsheet authors deduct the amount of acid they have added from Kolbach's RA and call that the RA
RA = alk -H/3.5 -∑_i Vi*ci*Qai(pHz)
Most spreadsheet authors are unaware (or choose to ingnore because it doesn't make a great difference) that the number of protons supplied by lactic and phosphoric acids depends on pHz so for them the amount of acid added is sumply the number of mmol of it and if we do that too then ∑_i Vi*ci*Qai(pHz) = ∑_i Vi*ci as Qai(pHz) is presumed to be 1. For further simplicity lets assume that there is only one acid so that we can represent the sum by just A, the number of millimoles of acid. Then
RA = alk -H/3.5 - A/Vw
with A divided by Vw as RA is per liter. Then
Vw*RA = Vw*alk - Vw*H/3.5 - A
represents the proton deficit of the mixture of mash water and added acid. The sum of the terms in the charge equation that represent these components is
Vw*Ct*(Qc(pHz) - Qc(pHs)) + Vw*(Qw(pHz) - Qw(pHs) + Vw*H/3.5 - A
Dividing through by Vw puts us on a per liter basis:
Ct*(Qc(pHz) - Qc(pHs)) +(Qw(pHz) - Qw(pHs) + H/3.5 - A/Vw
From this it is clear that if Ct*(Qc(pHz) - Qc(pHs)) +(Qw(pHz) - Qw(pHs) = alk then we could just substitute RA for it in the main equation. This would be great if we could get away with it because then, by ignoring bi and ci malt terms we would have
RA + ∑_i mi*(ai*(pHz - pHDi)) = 0 which is linear in pHz
RA + pHz*∑_i mi*ai - ∑_i mi*ai*pHDi = 0
and
pHz = (∑_i mi*ai*pHDi - RA)/∑_i mi*ai
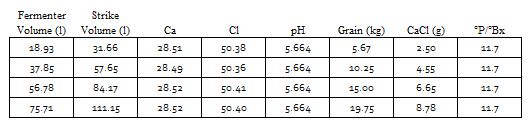
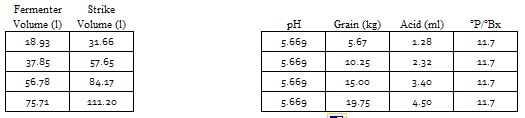
This is, I believe, what many of the spreadsheets try to do. Note that it even separates pHz into a sum of terms: one due to the malt and one due to the mash water. Of course it isn't going to work that well because we have ignored the non linearities in the malts and in the proton deficit from water alkalinity and ignored the fact that added acids don't actually donate 1 mEq of protons per mmol. So what do we do? We tweak the last formula to make things fit observed data better. I think the popular programs do this by comparison with reported errors from their users or beta testers. Given that with base malts the pH differences between pHDi and pHz are not that large ignoring their non linearities isn't going to cause that much error. With the colored malts (pHz - pHDi) will be larger but as these malts are used in quantity small relative to the base malt quantity perhaps the errors aren't that great but we have noted over the years that when HBTers report the wilder pH variations from Bru'n water the beer in question is often a dark one.
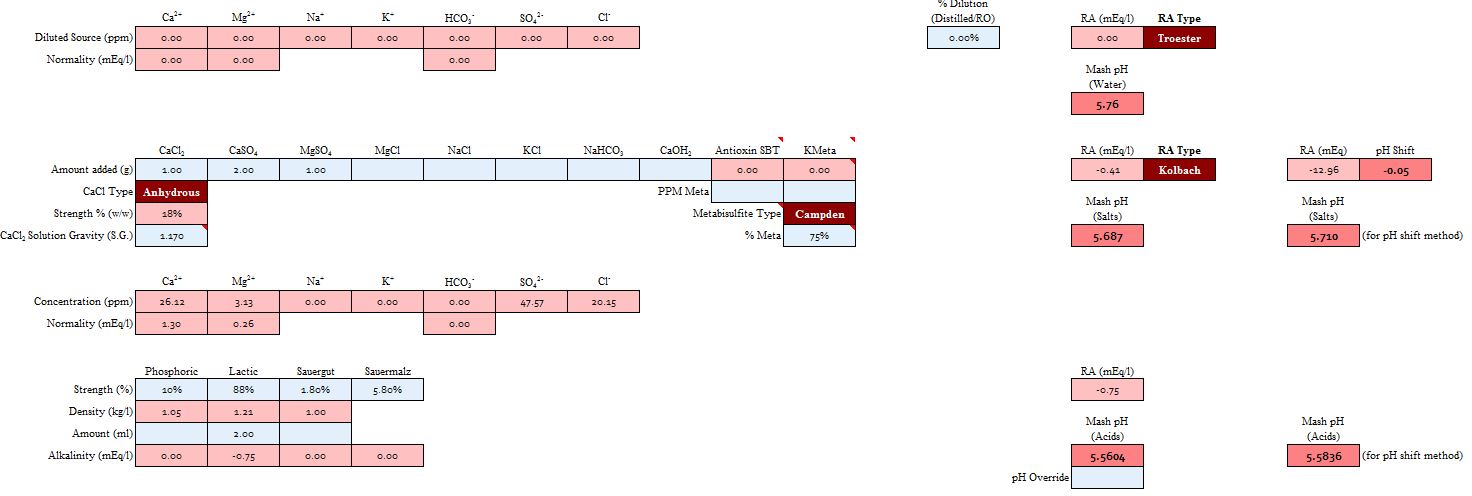
While Ct*(Qc(pHz) - Qc(pHs)) +(Qw(pHz) - Qw(pHs) ≠ alk there is a definite relationship between them. Ct is calculated from alk and pHs, the water's source pH. In fact
Ct*(Qc(pHz) - Qc(pHs)) +(Qw(pHz) - Qw(pHs) = f* alk
where f is a factor, usually around 0.9, that gives the proton deficit of the water/calcium/acid mix (still ignoring the dependence of acid strength on pHz) in terms of the alkalinity. Users of the RA based method will improve their pHz estimates if the use RA = f*alk -H/3.5 - A/Vw in computing RA with the catch being, of course, that f is a function of pHz and pHs. A couple of iterations will resolve that, of course, but the whole idea of forcing linearity is to dodge the recursion bullet. Values of f are found on the following graph:
View attachment 578805
A spreadsheet author could declare that the average brewer would be shooting for pH 5.4 and would have mash water of pH 7.5 and use 0.88 tweaking this in response to observed error reports. An important conclusion is that if your spreadsheet doesn't ask you for the source water's pH and especially if it asks for or prefers bicarbonate to alkalinity (forces you to convert an alkalinity report to a bicarbonate value before entering) be wary.








































![Craft A Brew - Safale BE-256 Yeast - Fermentis - Belgian Ale Dry Yeast - For Belgian & Strong Ales - Ingredients for Home Brewing - Beer Making Supplies - [3 Pack]](https://m.media-amazon.com/images/I/51bcKEwQmWL._SL500_.jpg)