Am I calculating my ph right?

[Silver_Is_Money]

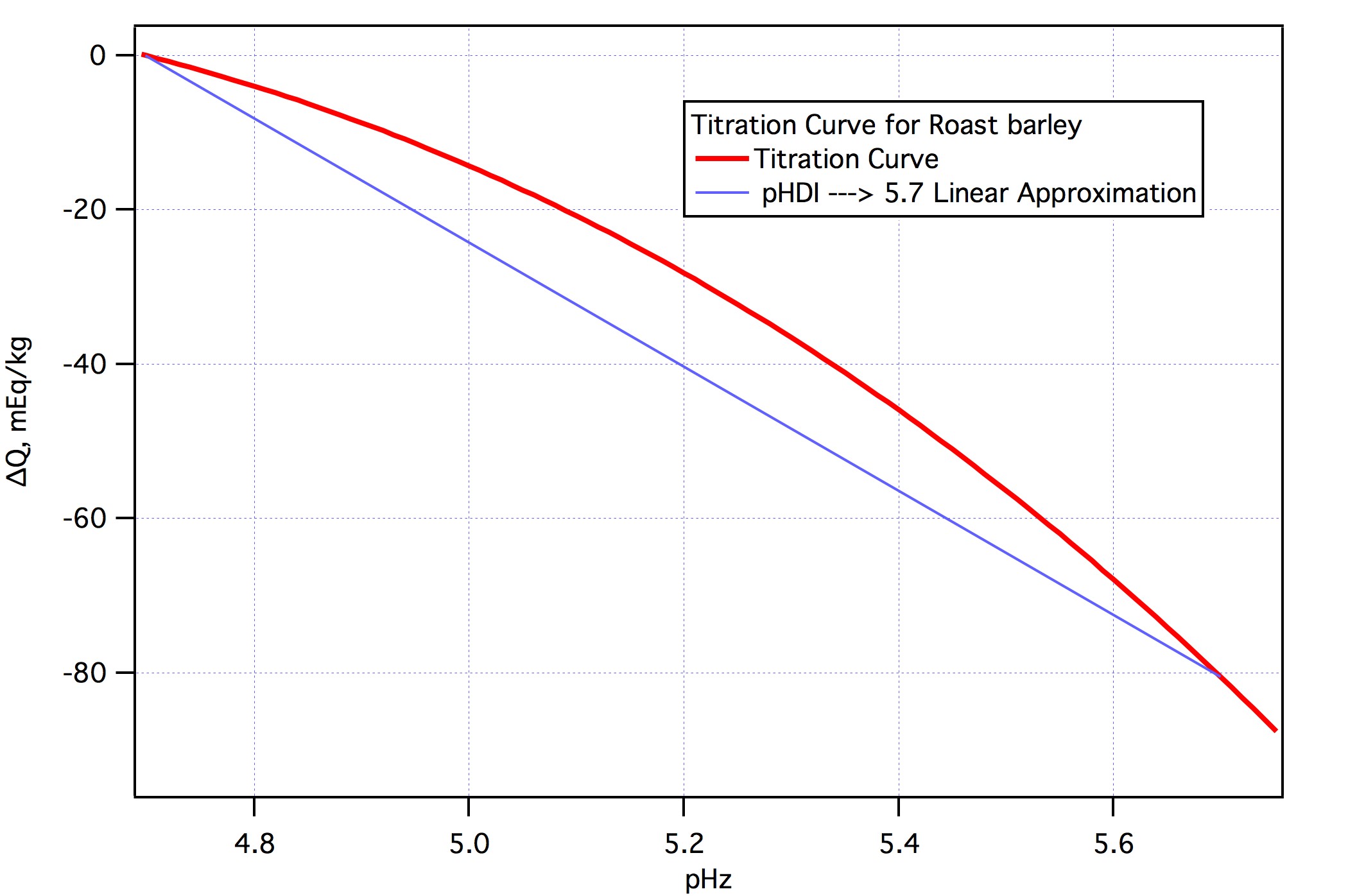
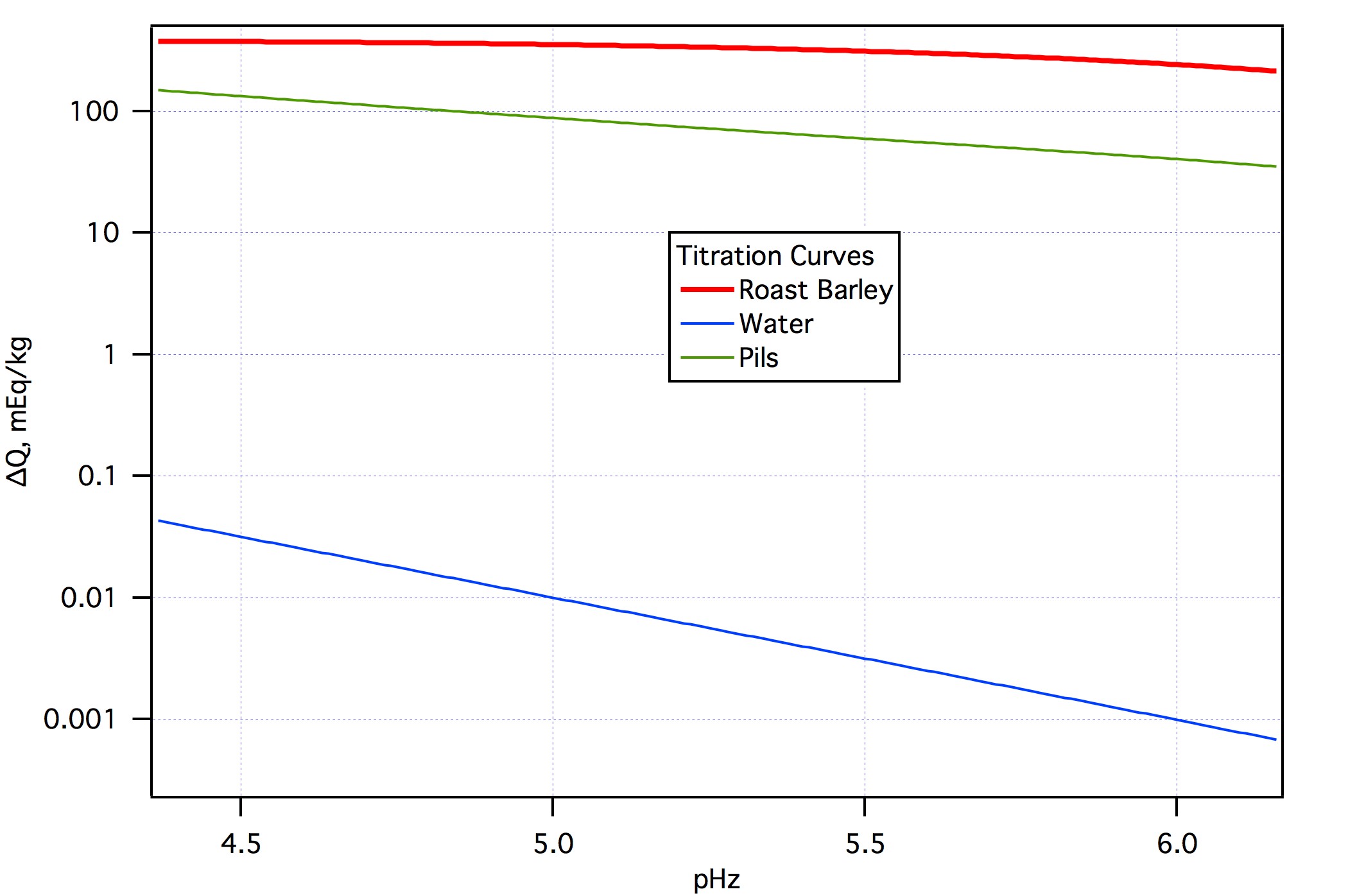
If Brewers Friend is used as in the very first of the OP's posts to this thread, but instead is set to the quick and easy "SRM color" mode, it gives effectively identical output as does the Kaiser Water Calculator, with my result for this Brewers Friend effort being the need for the addition of 16 grams of baking soda to hit a mash pH of 5.4.

This is not surprising, as Kai Troester, the very same Kai who created the Kaiser Water Calculator, contributed this section of the Brewers Friend online calculator.

But this leads to the conundrum of one BF method advising (perhaps, as I'm merely guessing here) 0.5 g. of baking soda to bump it from 5.37 to 5.4 pH, and another BF method offered within the same calculator advising the addition of 16 g. of backing soda, to bump it from 5.05 pH to 5.4 pH.

 

[MPBeer]

Never thought this thread would be this long! So, what I meant by chalk is "why should any one want to raise their ph if a grist bill with that much roasted grains have a ph of 5.37?". That seems pretty wrong, since I've heard that black malts lowers the ph down significantly, and I want to find a right program / sheet that can show me the closest mash ph.

So, the Kai's Calculator gets me more accurate result? English isn't my first language so I might be missing something from the conversation above.

Also my mash water is 5.3gal (20L) and it's a 5.3gal batch. A bit thick but my mash tun is only 30L so can't help Thanks!

 

[Silver_Is_Money]

So, the Kai's Calculator gets me more accurate result? English isn't my first language so I might be missing something from the conversation above.

Perhaps not. It's hard to imagine how a software program like Kai's that looks primarily at the ending color of the entire batch, albeit with a rather confusing (mainly as to how to properly apply it) modifier tossed in for the percentage of color that is derived from the roasted malts, can be more correct than a software solution which attempts to integrate the contributions for each malt or grain present. For the former case there is weak association between the final batch SRM and the overall acidity present, but then again, for the latter case there is also weak association between the grains colors and their individual acidities, so perhaps it's a wash as to who can stake more claim to validity.

All I can say at this juncture is: Stay tuned.

How many gallons of sparge water are you intending to use? To get a yield of 5.3 gallons in the fermenter you will need to use overall well more than 5.3 gallons of water. You will need sufficient water to overcome grain saturation water loss, as well as any other system and process losses, plus losses due to boiling.

*****As an aside, the Kaiser Calculator correctly (albeit confusingly) instructs as to how to derive the percentage of SRM color from roasted malts/grains, but the Brewers Friend instructions for this very same task (unless recently modified) are different, and fail miserably, and will lead to far different and likely catastrophic results. When I ran the Brewers Friend calculator in SRM mode, I used the Kaiser Calculator instructions, and not the Brewers Friend instructions. *****

 

[MPBeer]

Perhaps not. It's hard to imagine how a software program like Kai's that looks primarily at the ending color of the entire batch, albeit with a rather confusing (mainly as to how to properly apply it) modifier tossed in for the percentage of color that is derived from the roasted malts, can be more correct than a software solution which attempts to integrate the contributions for each malt or grain present. For the former case there is weak association between the final batch SRM and the overall acidity present, but then again, for the latter case there is also weak association between the grains colors and their individual acidities, so perhaps it's a wash as to who can stake more claim to validity.

All I can say at this juncture is: Stay tuned.

How many gallons of sparge water are you intending to use? To get a yield of 5.3 gallons in the fermenter you will need to use overall well more than 5.3 gallons of water. You will need sufficient water to overcome grain saturation water loss, as well as any other system and process losses, plus losses due to boiling.

*****As an aside, the Kaiser Calculator correctly (albeit confusingly) instructs as to how to derive the percentage of SRM color from roasted malts/grains, but the Brewers Friend instructions for this very same task (unless recently modified) are different, and fail miserably, and will lead to far different and likely catastrophic results. When I ran the Brewers Friend calculator in SRM mode, I used the Kaiser Calculator instructions, and not the Brewers Friend instructions. *****

Wish I can find my answer! I brewed that recipe with 3g each of gypsum and calcium chloride without anything that raises ph. Mash water was 5.3gal, and I added 4gal of water for batch sparge. I got 5~5.3gal of finished wort and now I'm fermenting it. Wish it doesn't taste to sour.

 

[Silver_Is_Money]

.....

After our discussion and development of A.J.’s troubleshooter, why even bother with Kai’s sheet?

Perhaps because the average home brewer will not have precise DI_pH values for every malt they will ever choose to use, let alone the requisite and also precise 3 point titration values for same.

But I use my own software, and I only consult Brewers Friend and Kai's spreadsheet (and others).

 

[Silver_Is_Money]

Wish I can find my answer! I brewed that recipe with 3g each of gypsum and calcium chloride without anything that raises ph. Mash water was 5.3gal, and I added 4gal of water for batch sparge. I got 5~5.3gal of finished wort and now I'm fermenting it. Wish it doesn't taste to sour.

Do follow up here and let us know how it turns out. Hopefully it will turn out great for you.

 

[Big Monk]

.....


Perhaps because the average home brewer will not have precise DI_pH values for every malt they will ever choose to use, let alone the requisite and also precise 3 point titration values for same.

This will be changing sometime next week. I'm going to be releasing a new brewing sheet with A.J.'s troueblshooter fully incorporated. I did an analysis of all the currently available malt titration values and came up with a representative set of malts with ph DI, a, b, and c values. I analyzed over 100 examples of titration data and of the 31 distinct classes of malt designations I created:

25% have a full compliment of pH DI, a, b, and c
51% have a partial compliment of pH DI, a, and b
49% have at the very least a linear relationship based on normalized values from D.M. Riffe's study

 

[Silver_Is_Money]

Excellent work RPIScotty!!! Blazing new trails!!!

When it comes out, it will be interesting to see how it turns out for the OP's recipe as to its baking soda need (if any) for mashing at 5.4 pH. I'm presently convinced the answer will be somewhere around 8.4 grams.

 

[FunkedOut]

Yes, with AJ's assistance, the buffering power of baking soda has been properly modeled now in Bru'n Water.

Excellent news!
Will there be a supporters version update soon?
I’m thinking this change is fairly recent, no?
Thanks.

 

[Silver_Is_Money]

The current score to bring the OP's recipe to 5.4 pH in the mash now reads as follows:
------------------------------------------------------------------------------------------------------------------
Brewers Friend in grist mode: Close to zero grams baking soda
Brewers Friend in SRM mode: 16.0 grams baking soda
Kaiser Water Calculator 1.58: 16.5 grams baking soda
Mash Made Easy testing version 2.15: 8.41 grams baking soda
Mash Made Easy released version 2.10: 7.99 grams baking soda
Bru'n Water 1.19: 13.8 grams baking soda
Easy Water 3.0.2: 0.85 mL Lactic Acid
MpH Water Calculator 3.0: 4.8 grams baking soda

Note that the OP selected 1.0L as the color of 2-Row base malt, and I have been using 2.0L for that malt.

Note that Bru'n Water 1.19 defaults CaCl2 to the anhydrous form (wherein most others chose the dihydrate form) so appropriately less was added than for the others so in the end the Ca++ was the same.

Note that MpH 3.0 yields a mash at 5.50 pH if 8.41 grams of baking soda are added.
Note that MpH 3.0 yields a mash at 5.65 pH if 13.8 grams of baking soda are added.
Note that MME v 2.15 yields a mash at 5.56 pH if 13.8 grams of baking soda are added
Note that MME v 2.15 yields a mash at 5.29 pH if 4.8 grams of baking soda are added
Note that Easy Water 3.0.2 yields a mash at 5.55 pH if 8.41 grams of baking soda are added
Note that Bru'n Water 1.19 yields a mash at 5.06 pH if 8.41 grams of baking soda are added
Note that Kaiser Water Calculator 1.58 yields a mash at 5.20 pH if 8.41 grams of baking Soda are added

All inputs (where applicable) were matching the snapshot of Mash Made Easy as seen above.

The average of all of the above calculators (wherein the 0.85 mL of Lactic Acid was entered as the negative value of -0.84 g. of baking soda) was 8.33 grams of baking soda.

 

[Silver_Is_Money]

Adding to the above, the very newly released Bru'n Water version 1.21 requires 17.2 grams of baking soda to bring the OP's batch to a mash pH of 5.4.

 

[ajdelange]

There is always going to be a problem with high colored malts because of their low pHDI's and the non linearity of malt titration curves. The charge change on a kg of malt is given by

∆Q = a*(pHz - pHDI) + b*(pHz - pHDI)^2 + c*(pHz - pHDI)^3

With a base malt pHz may be 5.4 and pHDI 5.7 so that pHz - pHDI = 0.3 but with roast barly, for example, pHDI = 4.7 and pHz - pHDI = .7. Then (pHz - pHDI)^2 = .09 for the base malt but 0.49 for the roast barley which is 5.4 times larger and the b term has, therefore, substantially more effect. Kai, IIRC, measured DI pH and the amount of acid necessary to get to 5.7 i.e. two points on the titration curve. I may not be remembering that right but I seem to recall discussions in which he said he wanted to be near mash pH but at a high enough value to encompass all likely mash pH's. The consequences, for roast barley, are shown in this graph:

The heavy red curve is the actual titration curve for this grain and the thin blue line the two point linear approximation. Looking at things from today's perspective it is clear that a linear approximation based on the ∆Q values at pHz = 5.3 and pHz = 5.5 would give a much better representation near actual mash pH than pHDI and 5.7 but at least that representation accurately represents pHDI which a 5.3 --> 5.7 fit wouldn't. In any case I think we are stuck with pHDI --> 5.7 in a program using Kai's data. The consequence is, because of the upward curvature of this titration curve, that the linear approximation will always overestimate the acidity of the grain (except at pHDI and pH 5.7) and thus require us to add more bicarbonate than is actually necessary and, in pH estimation, result in pH estimates which are too low. This I have noticed over the years of looking at peoples' reports on beers made with lots of dark grains. But then I really don't know if they are using models based on Kai's data or are ginning up linear approximations other ways. If, for example, one used a linear approximation tangent to the actual curce at pH 5.2 then it would underestimate the acidity of this grain at all values of pHz except 5.2, require less bicarbonate and give pH estimates which are too high.

With paler beers the preponderance of base malts swamp the non linearlty errors of the colored malt models and base malt models are not so strongly effected by ignoring b and c.

 

[Silver_Is_Money]

To my knowledge 'Mash Made Easy' differs radically at its heart from all others (including I believe the A.J. math model) in its application of base 10 logarithms to a determination of a grists overall pre-adjustment mash pH. My assumption in doing this is that if other chemistries involving titration can have their pH endpoints predicted by an application of base 10 log, and if the very pH scale itself is a base 10 log system, then why not similarly treat merged combinations of malts and grains as for many other titration chemistries with regard to their combined and amalgamated pre-adjustment pH?

I.E., if within a liquid chemistry system 10 gallons of water at pH 6 is merged with 1 gallon of water at pH 4, the resultant pH of the blend is 5, then why should not 10 Lbs. of malt at pH 6 and 1 lb. of malt at pH 4 also combine within a DI water mash to yield a pH of 5? This simple principle in essence is at the heart of Mash Made Easy. I doubt that any other software applies this thinking at any level. The simplicity of MME's method when compared to the mountains of mathematical complexities that form the heart (or engine) of other competing software is astounding. Yet, when compared side by side with the others, its output is generally highly in agreement. I'm not saying that one method is better than another, but in the end if both methods end up at the same place, then why not apply Occam's razor?

The essence of this is in the end merely another thought experiment.

 

[ajdelange]

I.E., if within a liquid chemistry system 10 gallons of water at pH 6 is merged with 1 gallon of water at pH 4, the resultant pH of the blend is 5, then why should not 10 Lbs. of malt at pH 6 and 1 lb. of malt at pH 4 also combine within a DI water mash to yield a pH of 5?

It works with water because water's charge is log linear (obviously) in the region you have chosen. It doesn't work with malts because because their charges aren't. The the titration curves below for roast barley (same as in No. 42), a pilsner malt and water are given with ∆Q relative to ∆Q(7) because it is the shapes of the curves we are interested in here. For a method combining pH's the three curves would all have to have the same slopes and it is clear that they don't. The roast barley curve isn't even a straight line.

Now you may argue that the curves aren't parallel straight lines but they are fairly close to being parallel straight line. This may enable you to work in some corrections that make a method of weighted combinations of pH values give approximate answers but the result will be just another spreadhsheet that give approximate answers.

The simplicity of MME's method when compared to the mountains of mathematical complexities that form the heart (or engine) of other competing software is astounding.

Yes, but the user of a spreadsheet doesn't care whether the math underlying that spread sheet is complex or not unless it is visible to him. He wants a robust system that gives him a good answer. A good spreadsheet is one that is complex enough to give good answers (however complex that may be) and hide those complexities from the user. And you can hardly call the math behind the robust solution complicated. Look at the spreadsheet cells. Now understanding why what is where may be a challenge for someone with little exposure to chemistry but the math itself is not complex.

Yet, when compared side by side with the others, its output is generally highly in agreement.

How does it compare with results obtained with the trouble-shooter?

I'm not saying that one method is better than another, but in the end if both methods end up at the same place, then why not apply Occam's razor?

To apply Occam's razor the pH combination method would have to be better than the complex method and that isn't likely to be the case.

You do have the trouble shooter available to you with which to check on your thesis. You'd have to modify it to accept a second set of malt parameters but it should be pretty clear how to do that.

 

[Silver_Is_Money]

The measure of validity for Mash Made Easy must be the measure of how it compares to a broad spectrum of batches mashed in the real world. Not how it matches up to other software.

 

[MPBeer]

The current score to bring the OP's recipe to 5.4 pH in the mash now reads as follows:
------------------------------------------------------------------------------------------------------------------
Brewers Friend in grist mode: Close to zero grams baking soda
Brewers Friend in SRM mode: 16.0 grams baking soda
Kaiser Water Calculator 1.58: 16.5 grams baking soda
Mash Made Easy testing version 2.15: 8.41 grams baking soda
Mash Made Easy released version 2.10: 7.99 grams baking soda
Bru'n Water 1.19: 13.8 grams baking soda
Easy Water 3.0.2: 0.85 mL Lactic Acid
MpH Water Calculator 3.0: 4.8 grams baking soda

Note that the OP selected 1.0L as the color of 2-Row base malt, and I have been using 2.0L for that malt.

Note that Bru'n Water 1.19 defaults CaCl2 to the anhydrous form (wherein most others chose the dihydrate form) so appropriately less was added than for the others so in the end the Ca++ was the same.

Note that MpH 3.0 yields a mash at 5.50 pH if 8.41 grams of baking soda are added.
Note that MpH 3.0 yields a mash at 5.65 pH if 13.8 grams of baking soda are added.
Note that MME v 2.15 yields a mash at 5.56 pH if 13.8 grams of baking soda are added
Note that MME v 2.15 yields a mash at 5.29 pH if 4.8 grams of baking soda are added
Note that Easy Water 3.0.2 yields a mash at 5.55 pH if 8.41 grams of baking soda are added
Note that Bru'n Water 1.19 yields a mash at 5.06 pH if 8.41 grams of baking soda are added
Note that Kaiser Water Calculator 1.58 yields a mash at 5.20 pH if 8.41 grams of baking Soda are added

All inputs (where applicable) were matching the snapshot of Mash Made Easy as seen above.

The average of all of the above calculators (wherein the 0.85 mL of Lactic Acid was entered as the negative value of -0.84 g. of baking soda) was 8.33 grams of baking soda.

Thanks a lot! That seems like a huge work! I like my recipe right now so I might brew this same recipe again with that addition. My beer (still fermenting) tastes a bit sour right now.. and I wish it tastes better with that ph adjustment.

 

[Silver_Is_Money]

How does it compare with results obtained with the trouble-shooter?

A.J., that will have to wait until RPIScotty comes out with his version of your trouble-shooter, and he finds a way to get it to run within LibreOffice.

All I can say for now is that (from loads of effort in applying a broad range of different recipes to a number of the currently available mash pH calculators, similar to as seen above) the outputs derived from Mash Made Easy version 2.10 (and my currently testing version 2.15, perhaps not far from release) seem to be generally well in line with the lot of them, all of which are using far more complex modes of internal operation. If my simple base 10 logarithm method is as hopelessly flawed out of the starting gate as you would seemingly imply, then I can't see why its output is in such generally good agreement with the others for mainstream type recipes.

And as you have stated above, the highest level of deviation between the others (verging upon radical, or essentially a total breakdown of any semblance of meaningful statistical correlation between them) jumps out quite noticeably when they are applied to extremely dark recipes which are loaded with an abundance (to perhaps overabundance?) of deep roasted malts. But even here Mash Made Easy in its most current versions (the very ones which have transitioned to the logarithm method of aggregate grist pre-adjustment mash pH determination) splits the average of their overall wildly conflicting outputs quite effectively right down the middle.

 

[ajdelange]

The measure of validity for Mash Made Easy must be the measure of how it compares to a broad spectrum of batches mashed in the real world. Not how it matches up to other software.

Ultimately, of course, that's true. In this case there are two parts to the problem. The first is feeding accurate data about the malt's properties to the candidate program and the second is processing that data in a way which gives a good pH estimate from the malt data. As we are interested in the acid base properties of the mash it seems reasonable that acid base titration curves would adequately characterize the malts and this has proven to be the case. We also have at our disposal a simple means for expressing those titration curves in terms of 4 parameters. So that leaves the methods used for converting a set of malt parameters into a pH estimate. We think we understand the science behind the mechanism that sets the pH. It has it's limitations but is fairly robust. A real chemist should have no trouble understanding it (though some here who claim to be real chemists haven't been able to grasp it) and therefore it represents a sort of gold standard to which algorithms that use purely empirical approaches like combining pHDI and mass numbers in some way that apparently gives at least reasonable answers can be compared. The troubleshooter is not another software for estimating mash pH. It is a tool for comparing how closely a candidate algorithm for mash pH prediction compares to a prediction based on the science as we (or really, I) now know it. At this point I don't think there is a better way to get a mash pH estimate which doesn't mean that there really isn't one. If you come up with an algorithm that uses only pHDIs and masses to estimate mash pH you are ignoring the fact that each malt has buffering characteristics and that it takes at least two numbers even to get a linear approximation. Now this doesn't mean that you method might not give decent results. If, for example, all malts had the same first buffering coefficient then you can come up with a scheme using only pHDI and mass but all malts do not have the same value for a and, in addition have unique values for b and c. Any algorithm that ignores this fact will produce an error. The question is as to whether the error so produced is tolerably small. This is where the 'troubleshooter' comes in. I think of it as a test instrument. Not suitable for the field but in the "lab". You can use it as a standard against which less robust algorithms can be compared.

Now if you have a perfect algorithm (even better than the troubleshooters's) and feed it pHDI, a, b and c which do not accurately model the malts being used then you still have a problem.

So the intent of the troubleshooter is to give you a credible means of processing malt titration data such that you can check on your pH (or other) algorithm's validity. It is not a mash pH prediction software package as it does much more than that and is not in a form that most brewers would be able to understand or use (though Scotty hopes to be able to insert the 'engine' part into such a program.

 

[ajdelange]

A.J., that will have to wait until RPIScotty comes out with his version of your trouble-shooter, and he finds a way to get it to run within LibreOffice.

Are you not able to cut and paste the column's into LibreOffice? I can always e-mail you a copy of the Excel if you PM me your address. I can even mod it to include a second malt input.

All I can say for now is that (from loads of effort in applying a broad range of different recipes to a number of the currently available mash pH calculators, similar to as seen above) the outputs derived from Mash Made Easy version 2.10 (and my currently testing version 2.15, perhaps not far from release) seem to be generally well in line with the lot of them, all of which are using far more complex modes of internal operation.

But as you noted in an earlier post the proof of the pudding lies in application of your algorithm against actual mashes - not in comparison to other programs. The other programs all dismiss aspects of the problem that we know are relevant and simplify other things such that their answers are suspect. Is your goal to offer another 'first generation' mash pH estimator? I thought we were working towards developing more accurate (i.e. will fare better when applied to actual mashes) 'second generation' spreadheets and calculators.

If my simple base 10 logarithm method is as hopelessly flawed out of the starting gate as you would seemingly imply, then I can't see why its output is in such generally good agreement with the others for mainstream type recipes.

First I'll have to admit that I don't really know how you combined 10 (gal), 6 (pH), 10 gal and 1 pH to come up with 5 but I do know that if you combine 10 gal of water at pH 5 with 1 gal at pH 4 you will get a mix with pH 5.00035 which is awfully close to 5. To get this number one computes the charge on water at pH 6 which is Qw(6) = 1000*(10^6 - 10^(6 - 14)) = 0.00099 mEq/L. Thus there must be 0.00099 mmol/L of the cation of some acid in there. Similarly for pH 4 Qw(4) = 0.0999999 mEq/L and, consequently 0.0999999 mmol/L of sulfate or chloride or something in that volume to keep the charge neutral. Combining 10 volumes of the first water with 1 volume of the second we'd have, in the case where the acids used to set the pH's were strong acids, a blend with ( 10*0.0999999 + 0.00099)/11 = 0.0099909 mmol/L of that acid'd anion. Because the acid we assume is strong there won't be a redistribution of species and all we need do is invert the charge function to find the pH of the blend, QWInv(0.0099909) = 5.00035 because the presence of 0.0099909 mmol/L of the anion implies that the positive charge on the water itself is +0.0099909 mEq/L. Were the acid used carbonic acid things would be quite different depending on how much carbo was dissolved in the two waters. For example, if we had 10 gal of water of alkalinity 100 ppm an blended it with 1 gal of water at pH 4 (which, of course, would have to be under CO2 pressure) the resultant pH would be 5.94. Carbonic acid isn't that strong an acid. Were the alkalinity of the larger volume only 50 then the pH of the blend would be 5.88. Were we to acidify a gallon of pure water to pH 4 with sulfuric acid and then blend that with 10 gal of water at pH 6 with alkalinity 50 the resultant pH would be 5.99. The amount of acid required to move the pH of alkaline water even a little is much more than the acid required to bring pure water to pH 5 can supply. Thus we see that the method you used to combine those 4 numbers to come up with 5 does not work even with water This is why I don't think your method shows much promise. There may still be something I'm not understanding here so please clarify if that seems to be the case.

 

[Silver_Is_Money]

A.J., when Mash Made Easy mashes 10 lbs. of DI_pH 5.5 malt combined with 1 lb. of DI_pH 4.5 malt this results in an output of 11 lbs. mashing at a pre-adjustment pH of 5.24 (rounded). This being for the most simplistic case of strictly DI mash water.

It follows the same standard base 10 log math model guidelines as for the case wherein if one was to make a simple blend of 10 liters of pH 5.5 acidified water combined with 1 liter of pH 4.5 acidified water, the end result would be 11 liters of pH 5.24 water.

Simple base 10 log. No fudge factors at all are presently being applied to the output to tweak what works for water into something that also works for malts and grains. If down the road such adjustment or tweaking factors prove to actually be required for malts/grains, they should prove to be relatively easy to work in later, malt class for malt class. But so far at least I'm leaning toward where such tweaking will not be required.

If the DI water mash case was instead for 10 lbs. of wheat malt at DI_pH 6.00 and 1 lb. of an extremely dark (say just for the sake of saying it, about at the hypothetical roasting level of 800 Lovibond) malt at DI_pH 4.00, the result in MME for this case would be 11 lbs. mashing at pH 5.00. This is also for the specific case of mashing in DI water.

This follows the same standard base 10 logarithmic math model guidelines as for the case wherein if one was to make a simple blend of 10 liters of pH 6.00 acidified water and blend it with 1 liter of pH 4.00 acidified water, the end result would be 11 liters of pH 5.00 water.

Then MME permits one to combine from 1 to 9 different DI_pH values of malts at any of their infinite potential for individual weights and does exactly as above.

I agree it is rudimentary, but oddly enough it does seem to correlate well with the ending output of other of such mainstream software that has been around far longer, and is highly assuredly to not be based upon such a simple model. And wherein specifically the ending output of which I speak is the required acid or base addition to move the mash to the selected target mash pH.

 

[Silver_Is_Money]

A.J., attached here is a link whereby two waters of differing pH's and volumes are blended to achieve a pH of 3.60. When I retain the same example pH's and simply convert the examples water volumes directly into weights of malts, and I then pass this example through Mash Made Easy, the output is also a pH of 3.60, so my math is just as for this example.

https://answers.yahoo.com/question/index?qid=20100514233814AAG3ITa

 

[ajdelange]

A.J., when Mash Made Easy mashes 10 lbs. of DI_pH 5.5 malt combined with 1 lb. of DI_pH 4.5 malt this results in an output of 11 lbs. mashing at a pre-adjustment pH of 5.24 (rounded). This being for the most simplistic case of strictly DI mash water.

And there are probably two malts you could find that would give that result.

It follows the same standard math model guidelines as for the case wherein if one was to make a simple blend of 10 liters of pH 5.5 acidified water and blend it with 1 liter of pH 4.5 acidified water, the end result would be 11 liters of pH 5.24 water.

OK, let's take 10gal of water at pH 8 and alkalinity 100 ppm and acidify, with strong acid (sulfuric or hydrochloric) to pH 5.5. Now lets take a gallon of water at pH 7 with alkalinity 50 and acidify, also with strong acid, to pH 4.5. Now we blend those. The resulting blend is 11 liters of water at pH 5.47 - not 5.24. In further acidifying the 10 gallons of 100 ppm alkalinity water at pH 8 which you initially have acidified (with 66.7 mEq of strong acid) to pH 5.5 further to 5.47 one requires only an additional 0.552 mEq of protons. In acidifying 1 gal of water with alkalinity of 50 and at pH 7 to pH 4.5 one only adds 3.785 mEq strong acid. In taking the pH of that acidified water back up to 5.47 it contributes 0.552 mEq protons. IOW, obeying the fundamental rule of combining acids and bases, the protons absorbed by the one entity (the 10 gal of water) must exactly equal the protons donated by the other (the 1 gallon). This differs, apparently, from what the 'standard math model guidelines say' so please tell me what those guidelines are.

Simple base 10 log. No fudge factors at all are presently being applied to the output to tweak what works for water into something that also works for malts and grains.

Except that it doesn't work for water. Common sense tells us that the final pH has to depend on the buffering of the things being mixed. With water buffering is the alkalinity. With DI water the alkalinity is the same (0) and so you are able to get an answer that is close to what your algorithm predicts. In the case of water coming out of someone's tap it doesn't work. But I still don't understand what you are doing with the simple base 10 logs to get 5.34 from 10 gal, 1 gal, pH 5.5 and pH 4.5. I do know that QwInv( (10*Qw(5.5) + 1*Qw(4.5))/11) = 5.24045 but Qw =Qw(pH) = 1000*(10^-pH - 10^(pH - 14)) but I don't see any logs in there. I do, however, see the antilogs. So, again, please tell me how you compute 5.24.

I agree it is rudimentary, but oddly enough it does seem to correlate well with ending output of other of such mainstream software that has been around far longer.

At this point I am struggling to see how, given that it gives the wrong answer for a simple blend of waters it could possibly give the right answer for malts. At this point it would seem immaterial as to whether it corresponds with what any other program predicts unless that program is the troubleshooter because I understand what that does and can see where all the protons go. And, as I expect you have already guessed the troubleshooter was used to come up with the numbers I have posted.

 

[Silver_Is_Money]

Multiple examples of hypothetical 2 differing pH blends as seen on the web yield blended pH answers exactly as for MME. Have you seen my provided link and its example that culminates in a blend at pH 3.60? MME matches this example precisely.

 

[ajdelange]

A.J., attached here is a link whereby two waters of differing pH's and volumes are blended to achieve a pH of 3.60. When I retain the same example pH's and simply convert the examples water volumes directly into weights of malts, and I then pass this example through Mash Made Easy, the output is also a pH of 3.60, so my math is just as for this example.

https://answers.yahoo.com/question/index?qid=20100514233814AAG3ITa

Question:
If a solution 500ml with pH 3.00 is mixed with a solution 1500ml with pH 6.00, what is the pH of the resulting solution?
My answer:
pH = 3.60

The "correct" answer, which differs from his only in that the very minor effect of the OH- ions is considered is
QwInv( (500*Qw(3) + 1500*Qw(6))/2000) ) = 3.60077

So yes, as I've said a number of times this method works when the water is pure and has been acidified by a strong acid such that the buffering is only that of the water itself. If there are any buffers in the waters being blended or if the acids used are weak then it doesn't work.

Actually the correct answer to the posed question is:

"I can't answer that question because you haven't told me about the buffering of the two solutions. If, other than the water's the buffering is 0 then we can proceed approximately as....."

 

[Silver_Is_Money]

A.J., Mash Made Easy also functions for the case of mash water of either existing or added alkalinity and mineralization. The model it uses to determine the downward pH shift due to Ca++ and Mg++ ions (or the upward pH shift due to alkalinity) in the mash water is one that I pulled from one (or more) of your posts to this forum (and thus why you appear among my credits). It appears to be Kolbach at heart. But it offers a range of buffer value tweaking which allows for varying the degree of the spreadsheets mineralization effect upon pH. Upcoming version 2.15 (or perhaps it will be 2.20 by the time I release it) will lower the mineralization pH impact of Kolbach to only 2/3 of its computed value, in keeping with your oft provided advice as seen on this forum which indicates that in the real world the downward effect of mineral additions upon mash pH is likely to be only somewhere between 50% and 70% of Kolbach. But just as for 2.10, there will also be a user tweakable buffering range that can move the spreadsheets impact of Ca++ and Mg++ mineralization upon pH both upward and downward a bit from the default. The impact of present mash water alkalinity in ppm's is I believe spot on, as when I substitute the mEq equivalent weight of baking soda (with your recent curve for it applied in version 2.15) and then drop the mash waters alkalinity to zero (or visa-versa), the mash pH (and adjustment to mash pH target) output results are identical.

It will indeed be interesting to see how far off my spreadsheet is vs. your model (as in the pipeline now from RPIScotty, with a promised release soon) once it becomes available. But then again it will also be interesting to see how well all of the other presently existing software for mash pH prediction stacks up against your model as well. As will it be to see how well your models predictions work in the real world for a range of beer SRM values and caramel, and roasted malt content situations, etc....

 

[ScrewyBrewer]

Now if you have a perfect algorithm (even better than the troubleshooters) and feed it pHDI, a, b and c which do not accurately model the malts being used then you still have a problem.

@ajdelange I understand what you're saying. If we are brewing a Kolsch using RO source water. Let's also say the DIpH values of the Pilsner and Vienna malts used are known. In addition to knowing the DIpH value (a) for the two malts the values for (b) and (c) are also known. Using your modeler to find the buffering of each grain then averaging their buffering capacity the accuracy of mash pH prediction is increased.

 

[ajdelange]

A.J., Mash Made Easy also functions for the case of mash water of either existing or added alkalinity

Let's check that. What does it say for the pH of a blend of 10 gal of water at pH 8 with akalinity 100 and 1 gal of water at pH 7 with alkslinity 50?

The answer is 7.86 - unsurprising as the 1 gal is only slightly acidic relative to the 10 gal and cannot be expected to move it's pH much.

...and mineralization. The model it uses to determine the downward pH shift due to Ca++ and Mg++ ions (or the upward pH shift due to alkalinity) in the mash water is one that I pulled from one (or more) of your posts to this forum. It appears to be Kolbach at heart. But it offers a range of buffer value tweaking which allows for varying the degree of the spreadsheets mineralization effect upon pH.

The protons emitted by the alkali earth/phosphate ions are treated exactly the same way as any other protons. They are distributed over mash anions in such a way that the net charge remains neutral. Their effect on mash pH depends, as it does with any proton loss or gain, upon the number of protons under consideration and the buffering of the mash. You have to accept that until you understand this you will never produce a robust product though you may be able to come up with something that is acceptably close under some conditions by empirical means. I can predict next weekend's weather in Alice Springs, NT (it will be fine) without doing a single computation of any kind i.e. no modeling of movements of air masses etc. But wouldn't it be better if I had a robust model of air masses etc. that got my accuracy up to 99%?

Upcoming version 2.15 (or perhaps it will be 2.20 by the time I release it) will lower the mineralization pH impact of Kolbach to only 2/3 of its computed value, in keeping with your oft provided advice as seen on this forum which indicates that in the real world the downward effect of mineral additions upon mash pH is likely to be only somewhere between 50% and 70% of Kolbach. But just as for 2.10, there will also be a user tweakable buffering range that can move the spreadsheets impact of Ca++ and Mg++ mineralization upon pH both upward and downward a bit from the default. The impact of present mash water alkalinity in ppm's is I believe spot on, as when I substitute the mEq equivalent weight of baking soda (with your recent curve for it applied in version 2.15) and then drop the mash waters alkalinity to zero (or visa-versa), the mash pH (and adjustment to mash pH target) output results are identical.

The ability to compute more probable proton emission from the calciummagnesium/phosphate thing and to have more accurate numbers for bnicarbonate proton absorption are, of course, steps in the right direction but their value is limited if you aren't considering mash buffering and, from what I've seen. you don't appear to be. Sort of like trimming your cases to precise length, weighing out the powder on an analytical balance, seating your bullets to the exact depth, checking runout... and then firing the cartridges in a rifle with a shot out barrel.

 

[Silver_Is_Money]

Let's check that. What does it say for the pH of a blend of 10 gal of water at pH 8 with akalinity 100 and 1 gal of water at pH 7 with alkslinity 50?

The answer is 7.86 - unsurprising as the 1 gal is only slightly acidic relative to the 10 gal and cannot be expected to move it's pH much.

EDIT: A.J., my program blends these waters to an alkalinity of 95.4545, but beyond that, in conjunction with an input of 11 gallons of mash water it can only then function upon various additions of malts in the presence of these 11 gallons of blended 95.4545 alkalinity water. Can you rephrase this query to accommodate my programs input capabilities? MME's only output capability is a prediction of the grists pre-adjustment mash pH in the presence of said water volumes alkalinity and/or mineralization, and the required acid or base to subsequently move this grist to a mash at a pre-selected pH target.

 

[ajdelange]

@ajdelange I understand what you're saying. If we are brewing a Kolsch using RO source water. Let's also say the DIpH values of the Pilsner and Vienna malts used are known. In addition to knowing the DIpH value (a) for the two malts the values for (b) and (c) are also known. Using your modeler to find the buffering of each grain then averaging their buffering capacity the accuracy of mash pH prediction is increased.

We need ∑∆Q(pHz) = ∑mi*ai*∆pH +∑mi*bi*∆pH^2 + ∑mi*ci*∆pH^3 =∑mi*(∑mi*ai/∑mi)*∆pH +∑mi*(∑mi*bi/∑mi)*∆pH^2 +∑mi*(∑mi*ci/∑mi)*∆pH^3

in which the factors in parentheses are the weighted averages of the individual buffering terms but why bother to calculate the averages when the sum just to the right of the = sign is the same and easier to compute?

Also pHDI is the DI mash pH, a is the linear buffering term coefficient, b is the quadratic and c the cubic. A malt is described by (pHDI, a, b, c).

 

[Big Monk]

We need ∑∆Q(pHz) = ∑mi*ai*∆pH +∑mi*bi*∆pH^2 + ∑mi*ci*∆pH^3 =∑mi*(∑mi*ai/∑mi)*∆pH +∑mi*(∑mi*bi/∑mi)*∆pH^2 +∑mi*(∑mi*ci/∑mi)*∆pH^3

in which the factors in parentheses are the weighted averages of the individual buffering terms but why bother to calculate the averages when the sum just to the right of the = sign is the same and easier to compute?

Also pHDI is the DI mash pH, a is the linear buffering term coefficient, b is the quadratic and c the cubic. A malt is described by (pHDI, a, b, c).

I calculate a weighted Δ Q value for each malt then sum then which then goes into the Δ Q total value for the sheet.