A thought experiment to test the general validity of available mash pH software

[ajdelange]

Thank you for posting AJ. I recreated your example spreadsheet. And honestly if you don't mind wondering how to use it to duplicate your scenario?

All you can do with it as is is enter different amounts of malt and DI water and then fiddle with pHz until Qtotal is as close to 0 as you can get it. This is the general technique for finding the pH of a mix of components. If we wanted to find the pH of a mix of this malt with water of finite alkalinity we would add cells to compute the charge change in going from the waters pH to pHz, add that charge change to the sum and, again, fiddle with pHz until we found the value that 0's Qtotal. If we wanted to find the pH of a mash with this malt, alkaline water and added acid we would add in the charge change for that acid and again find pHz that zeroes the sum.

 

[mabrungard]

Excellent discussion in this thread! I especially appreciate Mark Riffe pointing out the work that he and Mick Spencer completed. The pH response of flaked unmalted grains was certainly an unknown to me. I'm relieved to see that flaked barley responds similarly to malted base barleys and that most other flaked grains respond like base wheat malts.

I do wish that DI pH response was available for all brewing materials, but the fact is that its not. In addition, I find that 99% of homebrewers don't care to conduct DI pH trials for each of the myriad of grains that their recipes involve since most brewers don't have a reliable pH meter nor the extra time necessary to produce that data. Therefore, having the ability to fine tune a grain's pH response via a DI pH setting or a tweek in its color rating isn't going to be highly-valued adjustment to most brewers. But I agree that having that ability would sooth the geek in me.

I'm curious why Lawrence is so interested in pointing out what amounts to a 6.5% difference in acid demand when comparing normal and very dilute water/grist ratios? Given that there are far more opportunities for pH prediction discrepancies in actual water conditions, mineral additions, measurement error, and the big one...malt pH response, its seems a bit disingenuous to point this inconsistency out repeatedly in this thread. For the vast majority of brewers, that component is lost in the natural noise of mash pH prediction. Thanks for your concern, though!

 

[ajdelange]

I think the concern is that when they double the amount of malt and the amount of water as inputs to your program it tells them to use less acid which flies in the face of reason, of course but I admit I am still a bit confused.

 

[ajdelange]

Further to the simplicity of robust calculations you all got me started so here's another spreadsheet for you all to try and I hope you will as it can teach you a LOT about brewing water chemistry:

First column - the labels
Malt lbs
Water, gal
alkalinity, ppm
Water pH, pHs
Alk End point, pHe
Added Acid mEq
pHz

pHDi
a
b
c

Malt kg
Wter L
alk, mEq/L

∆Qmalt

r1e
r2e
f0e
f1e
f2e
QCe

r1Z
r2Z
f0Z
f1Z
f2Z
QCZ

r1s
r2s
f0s
f1s
f2s
QCs

Qwe
Qwz
Qws

Carbo Alk
Ct

∆Qwater/L
∆Qalk/L
∆Qmalt/kg

∆Qwater
∆Qalk
∆Qmalt
Added Acid
∆Q Total

Now the part that does the work
12.5
10
75
8
4.5
89.7164239728726
5.4

5.6227
-40.69
14.821
-10.008

=0.457*J1
=3.785*J2
=J3/50

=J10*(J7-J9)*J11*(J7-J9)^2+J12*(J7-J9)^3

=10^(J5-6.38)
=10^(J5-10.38)
=1/(1 +J20 + J20*J21)
=J20*J22
=J23*J21
=-J23-2*J24

=10^(J7-6.38)
=10^(J7-10.38)
=1/(1 +J27 + J27*J28)
=J27*J29
=J30*J28
=-J30-2*J31

=10^(J4-6.38)
=10^(J4-10.38)
=1/(1 +J34 + J34*J35)
=J34*J36
=J37*J35
=-J37-2*J38

=1000*(10^-J5-10^(J5-14))
=1000*(10^-J7-10^(J7-14))
=1000*(10^-J4-10^(J4-14))

= J16 -(J41-J43)
=J45/(J25-J39)

=(J42-J43)
=J46*(J32-J39)
=J18

=J15*J48
=J15*J49
=J14*J50
=-J6
=SUM(J52:J55)

When pasted into Excel the spreadsheet should look like this:

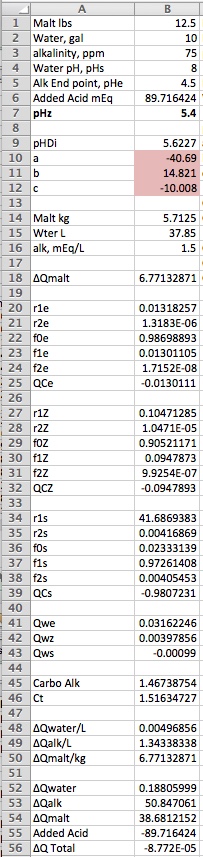
Now simple as this is it will allow you to robustly (no approximations about the relationship between bicarbonate and alkalinity for example - bicarbonate doesn't even appear anywhere):
1)Predict the pH of a mash given the entered amounts of malt (of the given parameters) and water (of given alkalinity and pH and of an acid or base addition
2)Determine the amount of acid or base to add to a mash using entered amounts of water and malt (with the appropriate parameters describing them.
3)Determine the amount of acid needed to adjust the pH of sparge water (just specify 0 for the lbs of malt).

The value of this spreadsheet is more pedagogical than practical. Obviously you would have to pretty it up extensively in order to present it to the public as a practical tool. It works in metric units of weight and measure and all calculation involving acid, base and charge amounts are in mEq/L which people don't seem to like. So it is really for those trying to write software who need to really understand how things work. Believe it or not I think 99% of brewing water chemistry is contained in these 56 lines.

I'll get into how to use it in a separate post.

 

[Silver_Is_Money]

I think the concern is that when they double the amount of malt and the amount of water as inputs to your program it tells them to use less acid which flies in the face of reason, of course but I admit I am still a bit confused.

Actually it is a doubling of the quantity of base malt for a fixed amount of mash water. 12.5 lbs. and then 25 lbs. of base malt, both mashed into 10 gallons of DI strike water, wherein the 25 lb. mash requires less acid to reach pH 5.4 than does 12.5 lbs..

I believe ScrewyBrewer has confirmed seeing the same result. If one allows that the acid addition result for 12.5 lbs. is correct, then the magnitude of the error in the acid addition required for 25 lbs. is on the order of greater than 50%.

 

[ajdelange]

RE the water calculation spreadsheet:
Enter the malt amount in pounds and the water amount in gallons in B1 and B2. They will be converted to metric units for calculation (B14 and B15). Enter the water's alkalinity in ppm as CaCO3 in B3 and its pH in B4. Alkalinity will be converted to mEq/L for calculation (B16). Enter the pH used by the laboratory when it measured alkalinity into B5. If the lab used the IOS procedure this will be 4.5 but Ward Labs uses 4.4. Add the amount of acid or base added as, respectively, a positive or negative number representing the total mEq added. I'll get to how to convert mEq to mL of a particular acid later.

In B9 enter the DI mash pH of the malt to be used followed by the linear buffering term in units of mEq/kg•pH in B10 and the second order and 3rd order terms in B11 and B12 if you have them. If you don't enter 0's for these two parameters. In practical use if one doesn't have these he must estimate them from malt color, malt type, a comparison to one of the malts measured by Kai Troester ....

Everything below B12 is calculated from the input data just discussed. Don't enter any data below B12.
In B18 the change in charge on 1 kg of malt in being shifted to pHz is calculated from the malt parameters.
In B20 and B21 the ratios of, respectively, bicarbonate to carbonic and carbonate to bicarbonate are computed at pHe. These ratios are then used to determine the fractions f0, f1 and f2, of carbonic, bicarbonate and carbonate species at this pH. These are in cells B22 - B24, finally, the charge on 1 mmol of carbo at pHe is calculated (-f1 - 2*f2) in B25. Cells B27:B32 contain the same information but for pHz and cells B34:B39 for pHs, the pH of the water sample.

Cells B41:B43 contain the charges on the water molecules them selves in 1 L of water at, respectively pHe, pHz and pHs. The whole of mash pH chemistry is determined by the changes in these charges as we go from one pH to another.

In B45 we take the change in charge between water molecules at pHe and at pHs and subtract that from the laboratory's alkalinity measurement. That charge difference represents the amount of acid that had to be added to the sample to establish the charge at pHe. It is the alkalinity of the water itself and must be deducted from the total acid addition in order to determine how much acid went to 'neutralizing' bicarbonate and carbonate in the sample. Thus is the Carbo Alk in B45.

If we take the amount of acid supplied to handle the carbo and divide by the charge difference on 1 L between pHe and pHs per mmol, we get the number of mmol of carbo in 1 L of the water. This is in B46.

By looking at the formulas in cells B52 and B53 you will perceive that these are simply the charge differences for the water molecules and carbo alkalinity both per liter (and per mmole of carbo in the latter case) multiplied by the number of liters of water and by the mmol carbo/L in the latter) to give the total charge differences for the mash for those components. We sum them up and add the charge difference from added acid to get the total charge change in shifting the malt from pHDI to pHz and the water (including its carbo) from pHs to pHz. The sum is in B56.

B56 must be 0. If it isn't we have either the wrong value for pHz or the wrong value for the acid addition or both. To get an answer from the spreadheet we tweak one or the other of these parameters to get B56 to as close to 0 as we can. If, for example, we want to know how much acid to add to this mash to get pH 5.4 we enter pH 5.4 in B7 and fiddle with B6 until B56 is small. It is much better to tell the Solver to adjust B6 until B7 is 0 but if you are terrified of the Solver, as many seem to be, you can get there manually pretty quickly too. Conversely if we want to see the pH with a given acid addition, just enter that acid addition and tweak pHz (or have the Solver do it) until B56 is near 0.

Now suppose the spreadsheet tells you you need 89.7 mEq of acid to get to pH 5.4 and you want to use lactic acid. If you understand what is going on in cells B20:B25 you will be able to figure out what to put into a couple of auxiliary cells to comput the charge on a mmol of lactic acid at pH 5.4 using the fact that it's pK is 3.86 (6.38 and 10.38 are the pKs of carbonic acid). Hint: use the same formulas as in B2025 but use 50 in place of 10.38 for the second pK of lactic acid in calculating r2. That will make r2 = 0 (effectively). As the charge on lactic acid is 0 when it's in the bottle the charge difference when you add it to your mash which is at pH 5.4 is just the charge at 5.4.

It should also be clear what one would need to do to add a second (and 3rd or 4th malt)

So play with this spreadsheet to see what happens, where the charges go etc. and you should come to a full understanding of the difficult part of brewing water chemistry. At least I hope so. I'm sure there will be quesrtions (if, in fact, anyone is really interested in this). Fire away.

 

[ajdelange]

Just couldn't resist as it's so simple and augmented the spreadsheet to accept an input of lactic acid and sodium bicarbonate. The label column is
Malt lbs
Water, gal
alkalinity, ppm
Water pH, pHs
Alk End point, pHe
Added Other Acid mEq
Added Lactic, mL
Lactic % w/w
Added NaHCO3, gm

pHz

pHDi
a
b
c

Malt kg
Wter L
alk, mEq/L

∆Qmalt

r1e
r2e
f0e
f1e
f2e
QCe

r1Z
r2Z
f0Z
f1Z
f2Z
QCZ

r1s
r2s
f0s
f1s
f2s
QCs

r1Lz
f0Lz
f1Lz
QLz
Lactic density g/mL
Lactic mmol/mL
Lactic Normality mEq/ml

Qwe
Qwz
Qws

Carbo Alk
Ct

∆Qwater/L
∆Qalk/L
∆Qmalt/kg
∆Qlac/cc
∆QNaHCO3 mEq/gm

∆Qwater
∆Qalk
∆Qmalt
Added Other Acid
∆Q Lactic
∆Q NaHCO3
∆Q Total


and the works are
12.5
10
75
8
4.5
0
8.27456389434625
88
0

5.4

5.6227
-40.69
14.821
-10.008

=0.457*B1
=3.785*B2
=B3/50

=B14*(B11-B13)+B15*(B11-B13)^2+B16*(B11-B13)^3

=10^(B5-6.38)
=10^(B5-10.38)
=1/(1 +B24 + B24*B25)
=B24*B26
=B27*B25
=-B27-2*B28

=10^(B11-6.38)
=10^(B11-10.38)
=1/(1 +B31 + B31*B32)
=B31*B33
=B34*B32
=-B34-2*B35

=10^(B4-6.38)
=10^(B4-10.38)
=1/(1 +B38 + B38*B39)
=B38*B40
=B41*B39
=-B41-2*B42

=10^(B11-3.856862)
=1/(1 +B45 )
=B45*B46
=-B47
=(-0.0000032247*B8 + 0.0026771)*B8 +0.99464
=1000*B49/90.08
=B50*B47

=1000*(10^-B5-10^(B5-14))
=1000*(10^-B11-10^(B11-14))
=1000*(10^-B4-10^(B4-14))

= B20 -(B53-B55)
=B57/(B29-B43)

=(B54-B55)
=B58*(B36-B43)
=B22
=-B51
=1000*(B36 +1)/84.01

=B19*B60
=B19*B61
=B18*B62
=-B6
=B7*B63
=B9*B64
=SUM(B66:B71)



Correctly copied and pasted you should see

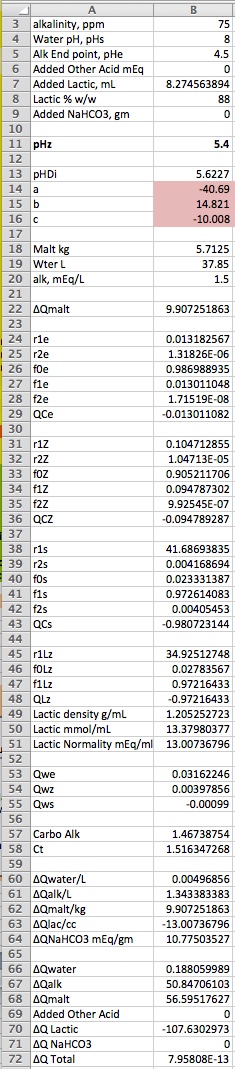
The things to notice are that there are new entries at the bottom for the charge changes for added lactic acid and for added sodium bicarbonate. And there are, of course, other cells where the r's and charge per mmol of lactic acid are calculated. As bicarbonate is bicarbonate whether from the water's alkalinity or added NaHCO3 we already had the carbo charge at pHz and all we need to realize is that the charge on the carbo in NaHCO3 is -1 mEq/mmol. The change when it is added to effect a shift to pHz is Q(pHz) -(-1) per mmol.

The use is as before. You enter values for everything you know and fiddle with what you don't know until ∆Qtotal is 0. Note that when lactic acid is involved you must specify its concentration as a percentage w/w. For an 88% solution enter 88 (not 0.88). As displayed it hs found the amount of 88% lactic acid needed to bring 12.5 lbs of pilsner malt mashed in water at pH 7 with 75 ppm alkalinity (ISO) to pH 5.4.

While this spreadsheet is obviously very simple it is recognized that perhaps understanding what is in each cell and why may not be simple. There is a certain threshold of knowledge and experience above which this is almost trivial and below which it doubtless seems comparable to particle physics. It took me a long time to cross that threshold and I am here to help any one who wants to to get across.

 

[ajdelange]

So let's use this newest spreadsheet to solve the problem in the OP (you remember the OP?).

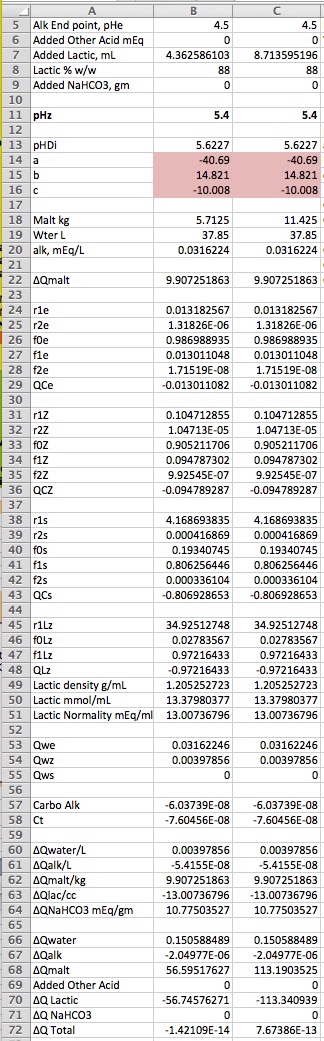
The two scenarios are the same (mash with 10 gal DI water) except that in the first we have 12.5 lbs malt and in the second 25. The first thing you may notice is that we have specified the alkalinity of the water as
1.58112 ppm. That is in fact the ISO alkalinity of DI water. How did we get that number? We told the solver to set B57, the amount of carbo in a liter of the water to 0 (the amount in DI water) by varying B3, the alkalinity. From this point on it is the same as before. Tell the solver to adjust the amount of lactic acid required to zero the total charge. The answer for the first scenario is 4.362 mL. Note that is is a little different from what I put in my first post. I had an error with regard to temperature correction (I think it was) for the pK of lactic acid and so that program computed a different normality for 88% lactic. Note that the normality for 20 °C is in cell B51. Doubling the malt changes the amount of required acid to 8.714, just a smidgeon less than doubling. Why is that? If we doubled the water and the malt the acid requirement would be just double. But we didn't double the water so we don't need an additional 0.15 mEq of acid for it.

 

[Silver_Is_Money]

A.J., as to the above spreadsheet, am I correct in understanding that the titration parameters provided are only valid for a single lot of tested 2-row base malt, and for other malts, and particularly more so those which radically differ from your chosen malt, the titration parameters required to be entered would be so noticeably different as to render gross error if one continued to attempt to use this spreadsheet 'as is' for such a different malt without also entering its highly specific titration parameters?

 

[ajdelange]

Yes, you are quite correct on that. For an additional malt paste in its parameters, use the formula to calculate ∆Q for that malt. Multiply by its mass (you'll need extra cells to enter that into, and to convert it to kg) multiply ∆Q by the mass of the new malt and enter that a new cell in the ∆Q summation area at the bottom. IOW, duplicate what's already in there for the example malt.

To add blending water duplicate what is there for the water now and add the new ∆Q into the totals area. Etc. The point is that whatever you add it is handled in the same way.

One other thought is that if you are concerned with the calcium shift you can calculate the total calcium (mEq) divide by 3.5 or 7 or whatever you feel is appropriate and stick that answer in the 'Other acid' cell.

This thing is a very powerful engine. Installed in a pretty spreadsheet it would be a valuable tool.

Note that what the spreadheet is doing is solving the equation

-x*Nac +y*Nb + ∆Qw + ∑_i ∆Qi +Lw*Ct*(Qc(pHg) - Qw(pHs)) = 0

of an earlier post. Were one writing a program rather than using a spreadsheet he would do the same thing - compute the sum and then 0 it by varying pHz.

 

[Silver_Is_Money]

A.J., as to my original scenario 1 and scenario 2 thought experiment, your new spreadsheet, though it yields somewhat differing results as to acid quantity, still clearly confirms that in transitioning from 12.5 lbs. to 25 lbs. of low Lovibond base malt (while holding the mash water quantity constant) there is a need to add very close to double the acid for 25 lbs. vs. 12.5 lbs. So in effect, it changes nothing with respect to the level of invalidity inherent within those existent spreadsheets available to the general public which do not also nearly double the acid added when making the jump from 12.5 to 25 lbs. of grist.

I must duly thank you for verifying that my initial thought experiment, though incorrect, was not all that far off (2.1%) despite some rather humorous flack which I have received along the way from another participant within this thread, and I also thank you for the fact that you have provided such a powerful tool (along with all of your other posts leading us to the way of truth which are embedded within this thread) for us to ponder over. You have gone exceedingly well beyond any expectations I might have had in the beginning with regard to solving this matter. Again, thank you!!!!

 

[ajdelange]

There were some errors in the numbers in my first post due to data entry (water akalinity) and other (lactic acid normality computation - how long has that been there?) errors in my old faithful spreadsheet which I caught thanks to the new one posted here. The correct numbers indicate an acid requirement of 0.151 mEq for the 10 gallons of water and 56.595 mEq for the malt. Thus the error caused by ignoring the water's alkalinity is only 0.151/(56.595 + 0.151) = 0.26%. I wouldn't call that level of error incorrect but as you know my philosophy is that as it is so easy to track the minutiae with tools like this spreadsheet why not eliminate these small error sources. Then we can focus on the errors that are not easily controlled like the errors in malt models confident that at least our computations are robust.

 

[cloudybrewer]

I've been following this thread since the start. While I don't understand a lot of the actual chemistry, I've learned a ton about the basic concepts of mash pH and how different mash components (grain, water, added minerals, added acid) affect the pH. Thank you to everyone who contributes! There may only be a handful of you responding to the thread, but there must be many silent readers like me who are better for it. I'm merely a student in a room full of teachers, but I've stumbled across something that I don't think has been addressed (in point 3 below).

I've been playing around with both my free version of Bru'n Water (BN) and Brewer's Friend (BF), running different scenarios through them to compare. I've used both calculators for actual brews, so I'm familiar with how to use them. And, yes, I duplicate Silver's outcomes of scenarios 1 and 2 in the initial post.

What I've learned about the two spreadsheets:
Using DI water and 1.7L malt for a mash
1. If the malt and water amounts are doubled, both calculators double the lactic acid requirement to reach the same mash pH (although, their requirements are different, for reasons already outlined).
2. If the water amount is held constant, doubling the malt results in double the acid requirements from BF, and decreasing acid requirements from BW (at a ridiculously thick mash, the requirement becomes 0).
3. If the malt amount is held constant, doubling the water results in a very slight decrease in acid requirement from BF and more than double the acid requirement from BW.

The discrepancy in point 2 has been discussed, but I don't believe point 3 has been addressed. Maybe the heavy hitters in this thread would like to weigh in. Using the math AJ provided in the very beginning, point 2 should result in very slightly less than doubling the acid requirement, and point 3 should result in a very slight increase in acid requirement. Correct?

Point 3 is especially important for full mash, no sparge BIABers like me, since this is exactly what we are doing. Take the same grain bill, and add nearly double the water to the mash ( 1.5 - 2 qt/lb vs 2.7 to 2.9 qt/lb). Adding similar amounts of acid vs. twice the acid to move from traditional to BIAB is quite a difference.

If ANYTHING I've done here is incorrect, please set me straight. I'm only here to learn. Everyone who has taken part in this thread has put a lot of time into helping guys like me, and I really appreciate it.

 

[Silver_Is_Money]

So in the end the simple thought experiment based upon an observation of the expected outcome for titrations of strong bases with strong acids in a carrier of DI water (which is generally considered to be a fully innocuous carrier that does not enter in and affect the outcome, with this being the very reason why such titrations are carried out within DI water in the first place) was off by only 0.26% when extended to beer brewing, with its system of malt and grain weak acids (some of which are basic with respect to the mash pH target, and are thereby in effect for mashing purposes to be considered weak bases).

My conclusions from this are as follow:
1) Mash Made Easy version 1.40 induced only 0.26% error in transitioning from scenario #1 to scenario #2 for a DI water mash due to the presence of the DI water itself. If MME has any greater in magnitude errors, as it likely does (subject to their future detection, followed by their future rectification), they are not by any means largely due to the water to grist ratio issue.
2) Mash Made Easy version 1.50, in matching A.J's earlier fix for a 2.1% error due to the water to grist ratio issue, is now slightly more in error than was version 1.40, and thus a version 1.60 must now be introduced to solve for 0.26% error due to the water to grist ratio issue rather than for 2.1% error.
3) If software like Bru'n Water (or any others built upon it as their foundation, such that its underlying math models are generally in the public domain) is radically in error with respect to its acidification solutions provided for scenarios 1 and 2 (and more specifically for scenario #2, if one allows that it is clearly more close to correct for scenario #1, and thus totally off for scenario #2) which are carried out within the most simple to solve case of mashing in nigh on innocuous DI (or high quality distilled or RO) water, then logically it will remain highly in error for any other type of water as well. This software appears to have serious issues with regard to its handling of the water to grist ratio issue.
4) Many to most other of the publicly available software packages meant to provide mash pH assistance are also likely off due to their handling of the water to grist ratio issue, and by more than 0.26%. Some are off by roughly the 2.1% factor, and some clearly by more than this. And even a privately modified package is likely off in this regard.
5) The most simple means to avoid the potential for software output error induced by attempts to solve for the water to grist ratio issue may be to ignore it (as did Mash Made Easy version 1.40). ???

 

[Big Monk]

Now all you have to do is actually brew a batch and compare. Thought experiments are nice but they say little about what actually happens when you mix hot water and malt. I've never seen a spreadsheet, my own included, that was on point without some sort of modification. Add malt variance, water variance, etc. and what you have here is an interesting survey of ideas that says little about an actual mash.

I would be more interested in how the various sheets perform in real life.

Great thread though. Sometimes all it takes is a bunch of people talking something out to get the wheels turning.

 

[Silver_Is_Money]

I'm kicking the tires on Mash Made Easy version 1.60 standard and 1.60 metric presently. I made the A.J. fix (of an A.J. fix), solving for the 0.26% error. I also made a correction to an error I discovered within my math model with respect to the pH reduction which one should expect to experience due to added Ca++ and/or Mg ++ mineralization. If I had not had to go in and fix it yet again, I would have likely missed this one, so I'm glad that A.J. made me go through this exercise twice, as I killed two bugs. Stay tuned for this upcoming release.

 

[Big Monk]

I'm kicking the tires on Mash Made Easy version 1.60 standard and 1.60 metric presently. I made the A.J. fix (of an A.J. fix), solving for the 0.26% error. I also made a correction to an error I discovered within my math model with respect to the pH reduction which one should expect to experience due to added Ca++ and/or Mg ++ mineralization. If I had not had to go in and fix it yet again, I would have likely missed this one, so I'm glad that A.J. made me go through this exercise twice, as I killed two bugs. Stay tuned for this upcoming release.

Just to be clear: this 0.26% error is an error in estimation, not actual brewery numbers, correct?

 

[Silver_Is_Money]

Just to be clear: this 0.26% error is an error in estimation, not actual brewery numbers, correct?

RPIScotty, the answer to your question is to be found in A.J's post #102 above. A.J. will need to tell you if he would expect to be able to actually see this small difference in a real world brewing session using his specific base malt. It may just be swatting flies.

Summing up A.J's latest revised results by scenario (for his specific malt):
1) Scenario #1 requires a calculated 4.362 mL of 88% Lactic Acid addition to hit a mash pH of 5.4
2) Scenario #2 requires a calculated 8.714 mL of 88% Lactic Acid addition to hit a mash pH of 5.4
3) The simple doubling of 4.362 mL yields 8.724 mL (vs. the correct answer of 8.714 mL for scenario #2)

 

[Big Monk]

RPIScotty, the answer to your question is to be found in A.J's post #102 above. A.J. will need to tell you if he would expect to be able to actually see this small difference in a real world brewing session using his specific base malt. It may just be swatting flies.

Summing up A.J's latest revised results by scenario (for his specific malt):
1) Scenario #1 requires a calculated 4.362 mL of 88% Lactic Acid addition to hit a mash pH of 5.4
2) Scenario #2 requires a calculated 8.714 mL of 88% Lactic Acid addition to hit a mash pH of 5.4
3) The simple doubling of 4.362 mL yields 8.724 mL (vs. the correct answer of 8.714 mL for scenario #2)

Fair enough.

What kind of a data set do you have for real world measured values from Mash Made Easy? Dozens of batches? Hundreds?

 

[Silver_Is_Money]

Fair enough.

What kind of a data set do you have for real world measured values from Mash Made Easy? Dozens of batches? Hundreds?

Admittedly only a handful of mash pH comparisons via feedback comments received from my chosen Beta test volunteers, and another handful of results from my own brewing sessions. Perhaps my only leg up (if it can be called that) might lie in the fact that best fit regression slopes for my various classification types of malts (slopes correlating DI mash pH values to Lovibond colors by malt class) were generated from a range of DI mash pH lab test results graciously given to me upon request by Briess for their line of malts, which includes multiple lots worth of DI_pH results for some of their malts (along side of actual tested Lovibond color, as opposed to their generic marketing Lovibonds as seen in a LHBS), and admittedly only a few lots worth of DI_pH test results (again, along with real lab tested Lovibonds) for others. For most classes of Briess malt, the best fit was a linear regression analysis, but for at least one major class a non linear regression fit their data best. Thus my DI-pH vs. Lovibond color slopes differ from Kai's in that he regressed data from his own malt titration tests along with what I would only assume to be presumed Lovibond colors, whereas I regressed actual Briess provided titration data for both DI_mash pH and real Lovibonds. Either way, my actual lab tested data sets and correlation assessments made to same in the real world are admittedly both quite limited. And the Briess data would admittedly make for a number of virtually scatter plots similar to Kai's. And I only have their DI_pH results to correlate to their Lovibonds, malt for malt. I have no triple titration data sets for acidifications to a range of pH values as I presume would be required by A.J.'s software solutions.

 

[ajdelange]

I've been following this thread since the start. While I don't understand a lot of the actual chemistry,

The basic concept here is quite simple. A mash consists of a complex mixture of a lot of components many of which are acids or bases (defined as things that either emit or absorb protons) and many of which aren't. Protons are interchanged between the acids and bases. When something acquires a proton it becomes more positively charged and when it looses one it becomes more negatively charged. The number of protons is fixed so that the sum of the proton gains must be equal to the sum proton losses so that the total of all the charge changes in the mash as its components are mixed must be 0. For things like carbonate and bicarbonate we have models that allow us to compute the charge change as a function of pH. For malts it is not so simple but we can measure the charge change as a function of pH. Thus we can put together a spreadsheet, such as the one offered here, which adds up all the charge changes at a trial pH value and by adjusting intelligently find the pH value which 0's the sum. There really isn't any chemistry in this statement. It's pure math. The chemistry comes in where you want to understand why the model for the carbo series is what it is and, of course, it is highly desirable that you do. That chemistry is really no more than an extension (Henderson - Hasselbalch) of the Law of Mass Action which is taught in high school chemistry (or was when I was in high school) but the extension usually doesn't come until later.

2. If the water amount is held constant, doubling the malt results in double the acid requirements from BF, and decreasing acid requirements from BW (at a ridiculously thick mash, the requirement becomes 0).

That's obviously a serious problem with BW and leads to the question as to how a program that can get this so wrong could give a correct, or close to correct answer in other cases. It seems, as has been hypothesized earlier, that Martin is somehow assigning the malt's proton deficit to the water. Perhaps this error is somehow compensated for such that things 'work' in a certain range of mash thickness. Kind of like the stopped clock that is right twice a day. In any case this is clearly a major problem with this program that needs to be addressed sooner rather than later especially as a fee is charged for it.

3. If the malt amount is held constant, doubling the water results in a very slight decrease in acid requirement from BF and more than double the acid requirement from BW.

The discrepancy in point 2 has been discussed, but I don't believe point 3 has been addressed.

We did discuss this a little somewhere in this thread. DI water (at pH 7) is a base relative to malt so adding more to a fixed quantity of malt will result in a slight (very slight because water is a weak base) increase in pH (from pH 5.62309 to 5.62348 when adding 20 gal as opposed to 10 gal water to 12.5 lbs of pilsner malt).

point 2 should result in very slightly less than doubling the acid requirement,

From 56.74581945 mEq to 113.3409954 mE, an increase of 99.7%

and point 3 should result in a very slight increase in acid requirement. Correct?

Correct. From 56.74581945 to 56.89634915 mEq i.e an increase of 0.2%

Technically, a program that predicts a slight decrease in the amount of acid required when water volume is increased is in error and is not using the algorithm implied by the first paragraph in this post. But as the actual increase is so small (0.2%) I think we can accept the result from a program that reports a decrease of similar magnitude. Can we measure our lactic acid to 0.2%. Using quantitative transfer techniques and Class A glassware yes but are we confident that the 88% lactic acid from the LHBS is 88 ± 0.2% ?

OTOH there is a serious problem with a program that demands double the acid when mash water volume is doubled while holding the grain amount constant. The ISO alkalinity of DI water is only 1.6 ppm as CaCO3 and to pH 5.4 it is only 0.2 ppm. I can't fathom what the model being used might be but clearly it needs to be fixed to reflect the actual chemistry.

Point 3 is especially important for full mash, no sparge BIABers like me, since this is exactly what we are doing. Take the same grain bill, and add nearly double the water to the mash ( 1.5 - 2 qt/lb vs 2.7 to 2.9 qt/lb).

Then I guess I'd advise people to stay away from BW until the problem is fixed. Obviously this thread got started because the originator had enough common sense to perceive that something was wrong but even he wasn't sure and that's why he started the thread. But there are lots of trusting souls that think that because something comes out of a computer it must be right.

 

[Big Monk]

Admittedly only a handful of mash pH comparisons via feedback comments received from my chosen Beta test volunteers, and another handful of results from my own brewing sessions. Perhaps my only leg up (if it can be called that) might lie in the fact that best fit regression slopes for my various classification types of malts (slopes correlating DI mash pH values to Lovibond colors by malt class) were generated from a range of DI mash pH lab test results graciously given to me upon request by Briess for their line of malts, which includes multiple lots worth of DI_pH results for some of their malts (along side of actual tested Lovibond color, as opposed to their generic marketing Lovibonds as seen in a LHBS), and admittedly only a few lots worth of DI_pH test results (again, along with real lab tested Lovibonds) for others. For most classes of Briess malt, the best fit was a linear regression analysis, but for at least one major class a non linear regression fit their data best. Thus my DI-pH vs. Lovibond color slopes differ from Kai's in that he regressed data from his own malt titration tests along with what I would only assume to be presumed Lovibond colors, whereas I regressed actual Briess provided titration data for both DI_mash pH and real Lovibonds. Either way, my actual lab tested data sets and correlation assessments made to same in the real world are admittedly both quite limited. And the Briess data would admittedly make for a number of virtually scatter plots similar to Kai's.

Hopefully you see where I am going with this.

I admittedly use an algorithm that is a hodge-podge of other people's work. I am an engineer by trade and my main area of expertise is in troubleshooting. I love excel and I love brewing calculations, so conversations like this are right up my alley.

However, we should be very cautious of singling out the work of other's for criticism when your own calculations have such an admittedly low pool of empirical results, as well as a such a narrow pool of malts used for modelling.

My collaborator has hundreds of batches in the bag with pH calcs that I prepared and we still have runs of 4-5 batches at a time where we have to tweak for various real world issues like lot variance, etc. All my water estimation calculations have a BW style backbone. I make certain key changes to the basic algorithm based on the empirical data pool we have and the results have worked for me.

The only way to judge the success of spreadsheet, program, etc. is to actually test it. With that said, and piggybacking on AJ's comments above, if a thought experiment like this points out a glaring error in a program, it should be presented in a way that isn't confrontational so the author has a chance to address it if he/she feels it is warranted.

 

[Big Monk]

As a general aside, one of the things D.M. Riffe and I discussed in our most recent e-mail exchange was the pH/RA slope term he is using in the MpH v3.0 calculator. That term is water to grain ratio dependent and we (my collaborator and I) found that we were getting errors between estimated values and real world values when biological or mineral acids were used.

We ended up removing the calculation in favor of the 0.17 constant value used in BW and the numbers lined back up with expected. After that change, there isn't a single value dependent on WTG ratio in the sheet. Not sure if that says anything about the problem you are seeing here, but i'll report it anyway.

 

[Silver_Is_Money]

Let me begin by stating that Martin has done zillions of times more of deep and tremendous beneficial value and good for the homebrewing community than I (being merely a retired back yard homebrewer) could ever hope to accomplish. A.J. is correct in his comments above, in that when I compared my Mash Made Easy results for scenarios #1 and #2 to those for a range of other spreadsheets and online programs, I was struck by the fact that none of them were simply doubling the scenario #1 acid required to achieve the scenario #2 solution, sans for my simple spreadsheet. But in undertaking this quest, one spreadsheet stood out from among the crowd and seemed to result in what I perceived to be a nonsensical solution. Thus I took my problem to this forum with the hope that A,J. would chime in, as at first I had no real idea as to how to go about solving this dilemma, or as to which software packages were correct, and which were not. I asked for other forum members to try and duplicate my results for various of the available popular software packages, and only two others eventually did so. But the programmer of the radical outlier software appeared to denigrate me within his replies to this thread, so if I have insulted him, he has appeared to have likewise insulted me, rather than do as I eventually asked and simply tell us his software's solutions for scenario #1 and #2. Rather than state that my thought experiment was in error and that this was clearly a consequence of my total misunderstanding of the matter, he could have discovered for himself (and then openly admitted) that his software has serious issues. I humbly apologize to Martin if I have somehow offended him personally within this thread.

 

[Silver_Is_Money]

Perhaps I should mention that my education also lies in the field of chemistry and that I spent 45 years working for several major well known chemical firms, up to and including at one brief juncture the management of multiple chemical synthesis departments (simultaneous with raising three children). But long ago, in conjunction with a job change, I took a turn to material planning and then I rapidly became a buyer/planner, and thus for most of my years in the chemical industry I didn't have to think much about the science and mathematics of chemistry. Then I got old and retired, and now I suddenly have time on my hands again, so I decided to develop 'Mash Made Easy', as well as return to active home brewing after an extended hiatus from brewing (for which my roots go back to the 80's). I wish I was young enough to still recall much of the chemistry education that I left well behind me decades ago. My dad used to tell me "Son, don't ever get old!" His advice didn't work for him, and it clearly isn't working for me.

 

[ajdelange]

A.J. will need to tell you if he would expect to be able to actually see this small difference in a real world brewing session using his specific base malt. It may just be swatting flies.

I did mean to comment on this and sort of did in No. 111. Obviously we are chasing some nits here as evidenced by the fact that I have to express pH's and acid amounts to precisions much higher than we can possibly hope to measure in order to be able to demonstrate that there are differences. But as I have noted before it is so easy to have the math right that there really is no reason not to and if we have the math right we can then fully focus on the malt model with the assurance that if we see a discrepancy between a pH prediction and a pH measurement that it came from a flaw in the malt model - not from the fact that our calculations don't handle mash thickness properly.

We assume that the models for acids and bases (strong and weak) are adequately modeled by their well known chemistry. There is, of course, some question here too. What really is the pK of lactic acid? How much is it shifted by the ionic strength of the mash? But as the models of general chemistry are good and easy to check up on we accept them (properly programmed) which reduces the problem of getting good pH estimates to obtaining an accurate representation of the malt's titration curve. I represent that titration curve by a 3 term Taylor series expansion about pHdi which has the obvious advantage that Qmalt(pHDi) = 0 thus making calculation of ∆Qmalt = Qmalt(pHz) - Qmalt(pHDI)= Qmalt(pHz) easy. Given the gentleness of malt titration curves 3 terms is plenty (and maybe even more than are necessary) so I believe that ∆Q = a*(pHz - pHDI) +b*(pHz - pHDI)^2 +c*(pHz - pHDI)^3 adequately expresses any malt titration curve that we may encounter in terms of the parameters pHDI, a, b and c. So when I speak of a malt model I'm referring to the set of parameters (pHDI, a, b, c). I think, given that we have the math right, that the challenge is in going from available malt data to pHDI, a, b and c. It is trivially easy to assert that we can get good (pHDI, a, b, c) by titrating the malt and curve fitting to get values for the parameters. It is much less trivial to do the titration properly. I describe in my MBAA TQ paper what that takes. It's quite a lot of work to get a sufficient number of points to be fully confident that (pHDI, a, b, c) accurately represent the malt. The maltsters are not going to do this work and so we look at easier ways to get numbers. The approach originally taken by Kai Troester was to take pH measurements at 2 pH's. His data allow us to obtain pHDI and a giving us (pHDI, a, 0, 0) as the model. This clearly isn't as good a model as (pHDI, a, b, c) but is it good enough? Joe Walts (a professional brewer) took 3 measurements and fit them with an expansion about pH = 0 but that's easily converted to an expansion about pHDI and thus gives a (pHDI, a, b, 0) model which isn't as good as (pHDI, a, b, c) but is better than (pHDI, a, 0, 0) but is it enough better to justify the extra work and is it good enough in comparison to (pHDI, a, b, c) that we can be confident in it? For the record, I use both Kai's and Joe's data when I haven't made a measurement myself.

The real challenge is to get around measurement at all. Lots of the programs try to deduce a Qmalt model from malt color or malt type. These aren't generally too successful. Recently awareness of the importance of pHDI has arisen and more and more of the spreadsheet/calculators now allow the user to enter that parameter which is often available from the maltster and brewers seem to be willing to make a DI mash pH measurement when it isn't. It is impossible to predict mash pH or determine the amount of acid needed for a given pH without at least (pHDI, a, 0, 0) and that means that a program must come up with a value for a somehow. I am not clear on how any of them do this. I think they may just use a constant value such as a = -40 mEq/kg•pH but at least one poster here (dmr) is aware of the importance of a good a value and has advocated obtaining it by 'titrating' with a 'fiduciary malt' (one whose a is known).

I've never seen a spreadsheet, my own included, that was on point without some sort of modification. Add malt variance, water variance, etc. and what you have here is an interesting survey of ideas that says little about an actual mash.

My goal is help you guys get your spreadsheets to the point where you are correctly handling "water variance etc." and Qmalt correctly so that you can concentrate on the accuracy of Qmalt wherein the real challenge lies.

I would be more interested in how the various sheets perform in real life.

There is absolutely no question that the real worth of a calculator is found where the rubber meets the road. But at the same time you don't need to do a test in the brew house to know that a program that tells you to double your acid addition when you add an (essentially) 0 alkalinity component to your mash should be avoided.

Sometimes all it takes is a bunch of people talking something out to get the wheels turning.

It cetainly got my wheels turning and I am grateful to you guys for kicking that off.

 

[ajdelange]

My dad used to tell me "Son, don't ever get old!"

Consider the alternative. I do every day.

 

[Big Monk]

The real challenge is to get around measurement at all. Lots of the programs try to deduce a Q model from malt color or malt type. These aren't generally too successful. Recently awareness of the importance of pHDI has arisen and more and more of the spreadsheet/calculators now allow the user to enter that parameter which is often available from the maltster and brewers seem to be willing to make a DI mash pH measurement when it isn't. It is impossible to predict mash pH or determine the amount of acid needed for a given pH without at least (pHDI, a, 0, 0) and that means that a program must come up with a value for a somehow. I am not clear on how any of them do this. I think they may just use a constant value such as a = -40 mEq/kg•pH but at least one poster here (dmr) is aware of the importance of a good a value and has advocated obtaining it by 'titrating' with a 'fiduciary malt' (one whose a is known).

One thing that has shown itself to be a pretty profound improvement is the inclusion of even a basic weighted average of based malt DI pH.

Back in 2014 or so when myself and The Beerery started playing around with revised calculations for his brewery, we were using what we called a "Malt Color Override", i.e. we had a cell next to the malt color input and we would bypass the malt color with a value that shifted the color based acidity calculation and subsequently changed the pH. It didn't take us long to see that we were better served leaving the color based acidity calculation alone and supplementing the internal global DI pH value with an individual DI pH value for each grain.

We made further strides when I brought the idea here and you made the suggestion that I use weighted average for DI pH of all base malts used. This made sense because at the time (still in use actually) we were blending base malts.

I am in the camp that says i'd love to be able to use the full (pHDI, a, b, c) model and have maltsters provide those values but I can't help but think that given the accuracy that most people can measure too, that the truncated (pHDI and malt color based first co-efficient) model may not only be light years ahead of what most programs are still doing, but also good enough for most of us.

 

[ScrewyBrewer]

....The only way to judge the success of spreadsheet, program, etc. is to actually test it.

This is exactly why I'm hesitant to make changes. The regression testing needed to confirm the accuracy of predicted to real-world pH values is significant (think years). I brew a lot of different styles of beer. They tend to use different grains as expected. Some not all the recipes' predicted and actual pH values come out the same. Taking notes on the outcome of each recipe then using them when brewing the recipe next time helps zero in on pH.

While admittedly this approach is intuative. The variance is not calculated by the spreadsheet. But you can 'read between the lines' to add or subtract acid and base as needed to get the actual pH closer.

 

[ajdelange]

I am in the camp that says i'd love to be able to use the full (pHDI, a, b, c) model and have maltsters provide those values but I can't help but think that given the accuracy that most people can measure too, that the truncated (pHDI and malt color based first co-efficient) model may not only be light years ahead of what most programs are still doing, but also good enough for most of us.

That's, IMO, exactly the sort of questions that need to be addressed - not whether alkalinity is adequately modeled by bicarbonate/61.