A thought experiment to test the general validity of available mash pH software

[Big Monk]

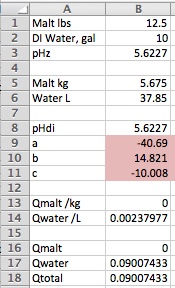
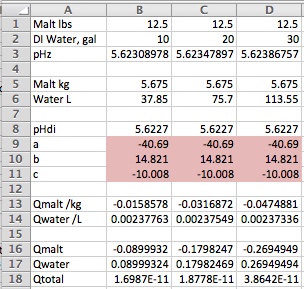
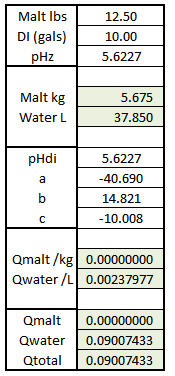
Reading along I was thinking this very same thing when this post came along. The basics here are really very simple to the point that the first spreadsheet I did that predicted mash pH accurately I put together during the presentation before mine at a MBAA meeting because I wansn't very interested in what the guy was saying but noted that he did include a spreadsheet in his talk and was thus able to illustrate his points and I figured my talk would benefit from that too. To use a simple spreadsheet, though, you have to have complete malt data and you aren't going to get that from the maltsters which means you have to get it from someone like me and a few other guys who are willing to make the measurements for you or do it yourself and as there is no ASBC sanction for this there is no MOA and so the data would not be standardized. In addition to having complete malt data you have to accept the 'model' represented by that data. If you don't have that data then you have to deduce it from what you do have which is information on malt type and malt color. Augmenting that data by giving the brewer the ability to enter pHDi is obviously a step in the right direction. Giving him the ability to put in the first (linear) buffering coefficient too is another step in the right direction and allowing him to enter the second order coefficient another. But now we expect him to understand what these terms mean or rather at least what the effect of modifying them might be and that's way beyond most potential users of a spreadsheet or program - even among professional brewers.

So I think it's fantastic that you guys are exploring all these avenues but you'll probably wind up where I did: 255 rows and 30 columns for the water sheet and 134 rows by 16 columns for the malt sheet. There's quite a lot of empty cells in there, though. It's got all kind of neat bells and whistle's of course and I can do almost anything water related with it but I stopped offering it to people years ago and would never consider doing so again (though I have given it to a few people).

I’ve set a goal for myself for this week to put a 31 Row/26 column sheet together of my current build along with volume and gravity for brewday. I’m of the opinion that if you are entering the grain bill anyway for pH estimation, you may as well track gravity and volume as well.

 

[Big Monk]

Here is a stripped down version of my modded MpH Sheet from Riffe:

https://drive.google.com/open?id=1XY7sdo1fUEBJTfZojLnQmGI4xROls1TY

Major assumptions are listed and a legend included to guide inputs.

 

[ScrewyBrewer]

Here is a stripped down version of my modded MpH Sheet from Riffe:

https://drive.google.com/open?id=1oRyyTJRPZJLso-GX4DKYV53qciRErjZw

Major assumptions are listed and a legend included to guide inputs.

Thank you for sharing RPIScotty. I look forward to comparing your changes to Riffe's MpH v3 and the others.

 

[Big Monk]

Thank you for sharing RPIScotty. I look forward to comparing your changes to Riffe's MpH v3 and the others.

The changes are pretty straightforward:

1.) Riffe's DI pH calculation goes away in favor of a weighted average of all base malt DI pH inputs;

2.) Riffe's pH/RA slope calculation becomes a static 0.17 (like BW);

3.) Troester/Kolbach RA denominator is selectable;

4.) Acid calcs are expanded to allow Sauergut to be modelled as low acid % Lactic;

5.) Acid calcs are expanded to include Kettle and Knockout additions;

6.) In my personal version (I didn't have a chance to add it here) I use a different calculation for acid malt reverse engineered from Kai's original Kaiser Water spreadsheet. Either way you shake it, I have found that acid %s of greater than 4% are required when using Sauermalz to account for the the pH in my test mashes. YMMV.

7.) Roastmalz acidity is variable based on user input.

 

[ScrewyBrewer]

RPIScotty using the following numbers in your modded sheet for 12.5lbs pilsner with DIpH of 5.72 in 10 gallons of RO water the mash pH is 5.72. When adding 5ml of 88% lactic acid the mash/acid pH is 4.71 whereas Riffe's sheet shows 5.51.

Also when adding 2g of CaCl2 your sheet shows mash/salts pH as 5.55, where Riffe's shows 5.68. Your ppm concentrations for show 55 for Ca and 96 for Cl, where the original sheet shows 14 ppm CA and 25 ppm for Cl. Either the modded calculations are off or I''ve inputed the data incorrectly.

 

[Big Monk]

RPIScotty using the following numbers in your modded sheet for 12.5lbs pilsner with DIpH of 5.72 in 10 gallons of RO water the mash pH is 5.72. When adding 5ml of 88% lactic acid the mash/acid pH is 4.71 whereas Riffe's sheet shows 5.51.

Also when adding 2g of CaCl2 your sheet shows mash/salts pH as 5.55, where Riffe's shows 5.68. Your ppm concentrations for show 55 for Ca and 96 for Cl, where the original sheet shows 14 ppm CA and 25 ppm for Cl. Either the modded calculations are off or I''ve inputed the data incorrectly.

Did you add strike volume as liters or gallons? I have it mislabelled as gallons.

Also, what color for the pilsner?

EDIT #1: I updated the link with a revised sheet. Couple of typo errors and a cell showing the strike volume in gallons as a reference.

EDIT #2: I ran the numbers with 5.67 kg (12.5 lbs) of grain Pilsner at 5.72 DI pH and 1.9 L color, 38 l (10.04 gal) of strike water. 2 g of CaCl and 5 ml of Lactic gives the following:

Grist pH = 5.72
Mash pH (w/ Salts) = 5.68, 2 g CaCl yields 14.37 Ca and 25.37 Cl
Riffe = 5.68, 2 g CaCl yields 14 Ca and 25 Cl
Mash pH (w/ Acid) = 5.41
Riffe = 5.51

Riffe undershoots when compared to empirical analysis of actual batches when using acids so the 0.1 pH delta here doesn't surprise me. It was the whole reason for using the static 0.17 pH/RA slope term. This change brought pH from acid contributions in line with what myself and my collaborator actually see in the brewery.

 

[ScrewyBrewer]

Ok thanks for explaining. Sounds good I will try the lastest update. I am using 2 L for the color.

 

[Big Monk]

Ok thanks for explaining. Sounds good I will try the lastest update.

It's likely to be closest to BW for comparable numbers, i.e. if you change the DI pH to 5.75 when comparing to BW that is. What's nice about the Riffe calculations is they are simpler to code and adapt into a brewing spreadsheet but with tweaks they give similar (or better) results than BW, especially if you implement the weighted DI pH averages.

Weighted average of DI pH alone makes a huge difference in estimated versus actual values.

 

[ScrewyBrewer]

It's likely to be closest to BW for comparable numbers, i.e. if you change the DI pH to 5.75 when comparing to BW that is. What's nice about the Riffe calculations is they are simpler to code and adapt into a brewing spreadsheet but with tweaks they give similar (or better) results than BW, especially if you implement the weighted DI pH averages.

Weighted average of DI pH alone makes a huge difference in estimated versus actual values.

What made you decide to use the Dihydrate form of CaCl2 over the Anhydrous form? 2g of dihydrate add ~19.0 ppm whereas 2g of anhydrous add ~14.0 ppm of calcium chloride.

 

[Big Monk]

What made you decide to use the Dihydrate form of CaCl2 over the Anhydrous form? 2g of dihydrate add ~19.0 ppm whereas 2g of anhydrous add ~14.0 ppm of calcium chloride.

It's the form most commonly found in stores, IIRC. My brewing space is in my basement which has low humidity so I typically don't have issues with my CaCl taking up excessive moisture.

 

[ScrewyBrewer]

It's the form most commonly found in stores, IIRC. My brewing space is in my basement which has low humidity so I typically don't have issues with my CaCl taking up excessive moisture.

After taking a closer look at the calcium chloride sold by LD Carlson they claim it is 'Anhydrous' because it isn't in liquid form. The product is readily available and sold at most homebrew stores I've used it for years. The small loose pellets looked the same as they did when first purchased even after being stored in my garage for over a year.

Based on what I've read if it were the Dihydrate form of CaCl being stored in my garage it would have absorbed water, become rocklike and lost potentcy. If the Dihydrate form of CaCl were to contain some Anhydrous form of CaCl then the Anhydrous form becomes the better option. Another unknown varible to deal with.

 

[Big Monk]

I’ve always used Dihydrate for calculations so, for better or for worse, it’s what my taste buds are acclimated to. YMMV...

 

[Silver_Is_Money]

I tested 2 separate bottles of LD Carlson CaCl2, and right after opening them for the very first time they averaged on the order of 94%, so not quite anhydrous. But my speculation is that it doesn't take too many openings in the presence of high humidity to get it to progress into the dihydrate form. I believe it needs to pick up well more moisture than the dihydrate form contains before it gets soft and then ultimately gets wet.

I left an opened bag of ice-melt sitting in a bucket in my garage one summer, and it turned into liquid goo.

An interesting experiment would be to place an open bottle of CaCl2 on a scale and see how fast it gains weight over time at ~50-60% humidity (give or take).

 

[ajdelange]

I've watched the numbers roll on a balance with CaCl2.xH2O in the pan. And I've measured various containers of it and found quite a bit of variability in x. In the Sticky on the subject I give a formula for the grams of CaCl2.0H2O in a liter of water as a function of it's specific gravity. A user makes a solution using CaCl2.?H2O and from the solution's SG learns how many grams of CaCl2 are in a liter of it. If he needs y grams of CaCl2 he just divides y by that concentration to get the number of mL of the solution he must measure out. Not only does this solve the unknown hydration problem but makes it possible to "weigh out" CaCl2 without a scale.

Clearly, in this context at least, calculators and spreadsheets should work in terms of the anhydride. Or at least offer radio buttons to allow the user to chose the hydration level he wants (to include the anhydride, of course).

 

[dmr]

Is he somehow conflating malt alkalinity and water alkalinity?

This is a conclusion I came to a long time ago (See Sec. 6.2 of my paper "A Homebrewing Perspective on Mash PH II: Water", which can be found on my blog).

BTW, you all may be interested in my latest paper "A Homebrewing Perspective on Mash pH III: Distilled-Water pH and Buffering Capacity of the Grist", which can also be found on my blog. The paper includes new data on a number of previously unmeasured malts. It also summarizes all the data I could find on the web. Happy reading!

I plan, at some point in the (not too distant) future, to totally redo MpH Water Calculator, with the calculations based on the results in this latest paper.

This thread has been quite entertaining!

Cheers!

 

[ajdelange]

dmr,

Had a look at the paper on your blog. Wow! A lot of hard work must have gone into that. I might mumble about using fiduciary malt as a basis for the 'titration', ignoring the (admittedly often small) non linearity of malt titration curves etc. but the main thing I want to point out to you here is that the basic notion of charge and proton conservation is equally applicable to mashes made with other than distilled water and can be used to predict the pH of mashes made with such water even when strong or weak acids or bases have been added for pH control. The basic idea is that all the items that go into the mash tun have acid base properties and are thus subject to a change in charge with a change in pH. You model the change in charge on a malt i as ∆Qi =mi*Bi*(pHg - pHi) and then solve ∑_i ∆Qi = 0 for pHg (note that pHg = pHz in my notation). A nit picker like me will, for the DI problem, calculate the charge change on the water itself, ∆Qw ≈ Lw*1000*10^(-pHg) (the charge on pure water is 0 as it has equal number of H+ and OH- ions) and add that in solving ∆Qw + ∑_i ∆Qi = 0 which, as it is no longer linear in pHg has to be solved iteratively but that's a triviality more important to me because it allows me to use the non linear model for ∆Qi = ai*(pHg - pHi) +bi*(pHg - pHi)^2 +ci*(pHg - pHi)^3 in which ai is the slope of the titration curve at pHi. To keep the benefits of the linear solution ∆Qw can be ignored as it is going to be a minor factor (a percent or 2 as we saw earlier in this thread) relative to the charge changes in the malts.

Now here's the essential point. If you add x mL of acid of normality Nac to a mash it will contribute Nac*x mEq protons and thus its charge goes from 0 (HCl has 0 charge, Cl- has a negative charge of -1 mEq/mmol). Thus the equation becomes -x*Nac + ∆Qw + ∑_i ∆Qi = 0. If you add y mL of a base of normality Nb then charge of y*Nb is removed and the equation becomes -x*Nac +y*Nb + ∆Qw + ∑_i ∆Qi = 0. Decrease in negative charge (malt where pHg < pHi, added base) requires protons and so is termed a proton deficit. In a case where negative charge increases (acid addition) protons have been give up and the substance that yielded them is responsible for a proton surfeit which is just a negative deficit. Everything here is in terms of deficits so bases and malts in which pHg < pHi are associated with positive charge changes in transitioning from their intrinsic pH to the target pH.

If there is carbonate alkalinity in the water it too is subject to a charge change of ∆Qc = Lw*Ct*(Qc(pHg) - Qc(pHs)) in which Lw is volume in L, Ct is the total mmol of carbonic, bicarbonate and carbonate in 1 L and pHs is the sample pH. The formulas for computing Ct and Qc from pHs, the water's original pH, and the alkalinity are given in the Sticky on bicarbonate/carbonate here. So adding this additional proton sink in we have

-x*Nac +y*Nb + ∆Qw + ∑_i ∆Qi +Lw*Ct*(Qc(pHg) - Qw(pHs)) = 0

to be solved for pHg. Now, of course, the linear dependence on pHg is gone (and ∆Qw ≈ Lw*1000*(10^(-pHg) - 10^(pHs) - 10^(pHg - 14) + 10^(pHs - 14)) as pHs is not longer necessarily = 7 so that there may be noticeable hydroxyl alkalinity) so that iterative (root bisection, Newton's method) solution is required if you are writing code or, if using a spreadsheet, the services of something like Excel's Solver tool is required. For some reason people will go to dramatic lengths to avoid using Solver or Newton or root bisection and if you are one of those then all is not lost. This is because for the majority of cases encountered by brewers Lw*Ct*(Qc(pHg) - Qc(pHs)) ≈ Lw*(2.09 - 0.22095*pHg)*alkalinity (alkalinity in mEq/L) and so you have, with this approximation and ignoring the alkalinity of the water molecules themselves, which you can only really do if hydroxyl alkalinity is low (pHs < 8 ?)

x*Nac -y*Nb + ∑_i ∆Qi - Lw*(2.09 -0.22095*pHg)*alkalinity = 0

which is again linear in pHg and so is easily solved for it but I encourage stepping away from the insistence on linearity as it is almost as easy to find the solution when the non linear models are used and the approximations used to force linearity go away. Another reason for doing this is that the normalities of weak acids and bases of which bicarbonate found both in source water and commonly used for pH control, depend on pHg. Most spreadsheets assume that the normalities of molar solutions of sodium bicarbonate, lactic acid and phosphoric acids are 1. They are approximately, but not exactly, so. To use the linear model requires us to consider them so.

In summary: malts, acids (strong and weak), bases (strong and weak) and even the water molecules themselves all undergo changes in charge when pH is changed. The charge changes are effected by transfers of protons among these mash components. As the number of protons is conserved the sum of the charge changes is 0. In the case of strong acids (HCl, H2SO4) and bases (NaOH, Ca(OH)2) the proton gains/losses are not dependent on pHg. In the case of weak acids (lactic, phosphoric) and bases (bicarbonate) the proton gains and losses are non linear functions of pHg and the same is true of the malts and water. In the case of the weak acids and bases we use we can approximate the proton losses or gains as 1 mEq/mmol of the added substance. We can also linearize the malt loss/gain by ignoring the non linear terms (or not measuring them) and we can ignore the charge change on water. These render the problem linear at the cost of having to introduce a handful of approximations. There is no need to do this as the solution to the non linear equation is simple:
1) Compute
QQ = -x*Nac +y*Nb + ∆Qw + ∑_i ∆Qi +Lw*Ct*(Qc(pHg) - Qw(pHs))
at pHg = 5.4
2)In a spreadsheet tell Solver to set QQ to 0 by adjusting pHg
3)In code use something like
function root()

variable pHlo = 3.5
variable pHhi =9
variable pHbi
do
pHbi = (pHlo + pHhi)/2
if(QQ(pHlo)*QQ(pHbi) < 0)
pHhi= pHbi
else
pHlo = pHbi
endif
while (pHhi - pHlo > .001)
return (pHlo + pHhi)/2
end

 

[ScrewyBrewer]

This is a conclusion I came to a long time ago (See Sec. 6.2 of my paper "A Homebrewing Perspective on Mash PH II: Water", which can be found on my blog).

BTW, you all may be interested in my latest paper "A Homebrewing Perspective on Mash pH III: Distilled-Water pH and Buffering Capacity of the Grist", which can also be found on my blog. The paper includes new data on a number of previously unmeasured malts. It also summarizes all the data I could find on the web. Happy reading!

@dmr thank you for both your recent and earlier work including your spreadsheets. I have been looking forward to reading and digesting "A Homebrewing Perspective on Mash pH III: Distilled-Water pH and Buffering Capacity of the Grist".

....I found 2 brand new bottles of LD Carlson CaCl2 sitting in front of my laptop. When I assayed one of the new bottles I found it to be 96% CaCl2 so it appears that the LD Carlson product is the anhydride which, over time, will, even in a closed bottle, pick up some moisture from the air.

@ajdelange thank you for posting your findings on the ClCa2 concentration of a new bottle of LD Carlson calcium chloride. And for confirming it is the anhydride form.

My goal is to make a maximum 20% w/w solution. This is my proposed procedure:

1. Measure (by weight) all of the CaCl2. Let's say it weighs 50g.

2. To get maximum 20% strength, I will weigh 5x50g=250g of distilled water and add the CaCl2 and mix until dissolved. I will then chill to room temp and measure the SG with my hydrometer. Let's say it measures at 1.150. Using some of the provided formulas this would mean the real w/w is about 16%, and that corresponds to about 190g/L.

3. Assuming I need 3.2g of CaCl2 to hit my numbers, I'd measure out 16.84mL (3.2g/190g/L) of this solution, and add it to the main water.

@schematix using your approach this is one experiment I look forward to doing and posting my results, thank you.

 

[ajdelange]

If anyone read No. 76 before reading this, go check it again. Done late last night it had several errors and I have added some other new stuff too.

 

[ajdelange]

I'll just point out that the first formula in the Calcium Chloride Sticky gives grams per liter directly from SG

g/L = -684.57 + 175.12*SG + 509.45*SG*SG

For sg 1.150 it returns 190.566 grams/liter. No need to calculate g/l from w/w.

 

[Silver_Is_Money]

Since pH is the concentration of protons in solution, it should be apparent that altering the mash's water/grist ratio will proportionally alter the pH.

I trust these explanations will help you understand the errors in your thought experiment.

Perhaps the key to the error in Martin's thinking lies within his choice of the word "proportionally" as seen above. Log base 10 systems such as pH are anything but proportional, if what he implies in this is conventional linear proportionality. If one takes 1 liter of pH 4 water, it requires dilution to 10 liters with pH 7 DI water to move it to pH 5. A 10 fold increase in the water. But within typical homebrewing I can only see perhaps the doubling of the DI strike water, as might be the case for transitioning from strike and sparge to BIAB with no sparge.

But the above aside, what we have actually been discussing here (within scenario #1 and scenario #2) is effectively a titration, with the DI strike (or mash) water used as merely the carrier within which to perform this titration, and with the quantity of the strike/mash water always held constant.

If one was to place 10 mL of 0.1N NaOH (a strong and thereby fully dissociating base) into 1 liter of DI water, the first expectation would be that titration to neutrality will require 10 mL of 0.1N HCl (a strong and thereby fully dissociating acid). And if the same quantity of the same base was to be placed instead into 2 liters of DI water carrier, one would still expect titration to neutrality to require (on first good approximation) 10 mL of the same acid.

For the #1 and #2 scenarios of his this thread, the concentration of the DI mash water is never altered. Only the quantity of the "base" malt added to the water has been doubled. If the specific case of NaOH and HCl as seen above was changed to read 20 mL of 0.1N NaOH added to 1 liter of DI water, one would nominally expect to find that titration to neutrality requires 20 mL of 0.1N HCl, or a precise doubling of the acid to neutralize the doubling of the base, to within a fairly high degree of reason (with this line of reasoning being the inspiration for my "thought experiment").

That the DI water doubling does actually play a small roll (as revealed by A.J.) would likely be detected if the detection equipment employed was precise enough to notice the difference, but my simple thought experiment involving scenarios 1 and 2 came directly from my contemplation of the rudimentary NaOH and HCl chemistry as seen directly above, and my thought experiment leads to only a small 2.1% error when scaled up to the brewing scenario #1 and brewing scenario #2 examples (as confirmed by A.J., whereby 5 mL transitioning to 9.89 mL in reality deviates from a simple line of reasoning that quasi-empirically implies 10 mL on first thought by the stated 2.1%).

I do now understand my error in my thought experiment, but I'm glad that its magnitude is (or rather was, with this having been rectified) essentially nigh-on inconsequential. The real and serious magnitude of scale in error seems to lie within Bru'n Water's reduction of the acid titrant projected to neutralize 25 lbs. of "effectively basic with respect to a mash target of 5.4 pH" malt vs. the quantity of the same acid that it requires to neutralize 12.5 lbs. of the same base malt within the exact same amount of deionized (DI) water carrier (assuming fully here that I'm using this software correctly in my attempt to use it to solve for the acidification required to satisfy both scenario #1 and 2). Such error (if truly present) does not appear to be inconsequential.

 

[Silver_Is_Money]

I should have added to the above that the DI water carrier itself likely plays a larger part within systems of weak acids (one of which I'm taking the full liberty to consider basic with respect to typical mash pH targets, with this being the base malt), so the Achilles heel (2.1% error) of correlating beer brewing to my simple thought experiment (such that my thought experiment is linked to the interactions of strong [or fully dissociating] acids and bases) is likely rooted here.

 

[ajdelange]

He is right that the mash pH shift is proportional to thickness in a DI mash. If we mash 12.5 pounds of a particular Pilsner malt with 10 gal of DI water we estimate pH = 5.628. Add another 10 gal and we expect the pH to go up to 5.633 as while the number of protons that go to the water is very small it is still approximately twice what it was before and weak though the base H2O may be there is now twice as much of it in the mash. Add another 10 gal and the estimated pH goes up to 5.639 i.e. up by about the same amount as it rose when adding the second 10 gal so the shift is indeed proportional to the amount of mash water but it is tiny: 0.005 pH per 10 gallons. We certainly could not, by any stretch of the imagination, say that altering the water amount proportionally alters the pH itself.

 

[Silver_Is_Money]

The extremes of Congress Mash (or DI_mash pH) for batches of Pilsner class 2-row barley malts may range as high as around pH 6.0 and as low as around pH 5.5.

I have Briess data which shows at least one batch of their Pilsner malt with a recorded DI_pH of 5.83.

Weyermann published an example of the effect of adding acidulated malt to one of their base malts with a 5.84 DI_pH, and some of their finest low Lovibond Pilsner barley malts may on occasion achieve a DI_pH of 6.

I've seen Maris Otter pale malt data indicating 5.77 for DI_pH for one lot.

Wheat malts can in some cases approach a DI_pH extreme of nearly 6.2. Briess data I have shows 5.89 for one relatively recent lot. The nominal here may be on the order of pH 6.

Programs must allow for flexibility with regard to a base malts DI_mash pH, as the strike water acid required to bring a "real world" low Lovibond 2-row single malt mash to pH 5.4(ish) can be as much as perhaps +/- 50% or more of the nominal software output advice if the program one is using considers only a 'mid-range' fixed initial base malt DI_mash pH with regard to Lovibond color.

 

[ScrewyBrewer]

Programs must allow for flexibility with regard to a base malts DI_mash pH, as the strike water acid required to bring a "real world" low Lovibond 2-row mash to pH 5.4(ish) can be as much as perhaps double or half of the nominal software output advice if the program one is using considers only a 'mid-range' fixed initial base malt DI_mash pH with regard to Lovibond color.

The onous to provide accurate DIpH values to drive that type of program lies either with the program's users or it's creator. Based on my personal experience consitently accurate DIpH values for each grain is non-existent. If a database of accurate DIpH values existed a program could access that data and consistently increase their predicted pH value accuracy. As long as the database was regularly updated with DIpH data changes.

Until that day hopefully comes pH prediction by grain color will play a useful role. ezBrewingWater was my first atempt at predicting mash pH using DIpH values. But a lack of access to valide DIpH values changed my approach to use grain color instead. ezRecipe my second attempt combines complete beer recipe design and mash pH prediction. The idea was to make it easy to learn and use but still approachable for users.

 

[ScrewyBrewer]

If we mash 12.5 pounds of a particular Pilsner malt with 10 gal of DI water we estimate pH = 5.628. Add another 10 gal and we expect the pH to go up to 5.633 as while the number of protons that go to the water is very small it is still approximately twice what it was before and weak though the base H2O may be there is now twice as much of it in the mash.

AJ I must be entering something incorrectly. Trying this in 4 different spreadsheets I am not seeing the same results. I see the pH values either decreasing slightly of staying the same when adding 10, 20 or 30 gallons of water.

 

[ajdelange]

If, when doing his Congress mash, the maltster did 3 more mashes the same as the Congress but with acid added at the rate of 5, 10 and 15 mEq/kg and measured the pH of each and fit a curve through the pH vs mEq data he could then read out the mEq values at round values of pH and make a table like the following (which characterizes Weyermanns Pils)


pH mEq/kg
5.62 0
5.50 5.3
5.40 10.0
5.30 15.1

If he put that table on each malt sack then the math to compute the acid needed for a desired pH for this model involves a trivial interpolation of the mEq/kg numbers between the two closest pH values in the table followed by multiplication by the mass of this particular malt. Doing the same for each malt gives the total acid or base. The table on a 600L black malt sack might look like this

pH mEq/kg
5.60 -72.0
5.50 -63.4
5.40 -55.1
5.40 -46.9
4.70 0

Given this data and the knowledge that the acid requirement for water alkalinity is about 90% of the alkalinity (per liter at pH 5.4, 92% at pH 5.3 and 87% at pH 5.5) a brewer can pretty easily come up with an estimate of the acid needed that is at least accurate enough to guide him through a test mash. Of course the acid required for the water can be easily and accurately calculated from the alkalinity and water and target pH's using the charge method.

A competent spreadsheet or calculator author will know how to turn the proposed malt sack table into the full malt model (∆Q = a*(pHg - pHi) +b*(pHg - pHi)^2 +c*(pHg - pHi)^3) and thus use the data for mash pH prediction.

Well, the maltsters aren't going to provide that table, at least not in my lifetime, but that doesn't mean that motivated brewers can't do exactly what the maltsters should do.

 

[Silver_Is_Money]

AJ I must be entering something incorrectly. Trying this in 4 different spreadsheets I am not seeing the same results. I see the pH values either decreasing slightly of staying the same when adding 10, 20 or 30 gallons of water.

On page 1 of this thread I mentioned Kai's findings that thinner mashes have a bit higher mash pH's and thicker mashes have a bit lower mash pH's. This is in agreement with A.J's pH shifts as seen in his post above. But such minuscule pH differences are not significant with respect to juggling a myriad of unknowns.

I can only speak for Mash Made Easy. My software is admittedly quite quasi-empirical at its core (and quite likely more-so than most in this regard). I have tried very hard to design it to empirically reflect much of the "reality" as seen by the (to my comprehension, rather intimidating) math models of a genius on the order of A.J. DeLange or Kai Troester, but through the application of far more simple and often far more empirical means. My software is by no means perfect, and I make no claim that it is. Your findings as quoted above being but one discovered example of this. I'm certain that flaws can be found within the output derived via my software, and particularly more-so if oddly extreme situations not often (to perhaps not ever) expected to be experienced on an average brewing day are thrown at it.

That said, if one looks at the slope lines drawn within the myriads of data charts provided by Kai Troester, one sees that his formulas are often derived from linear regressions drawn through what almost appear to be scatter charts of real hard core and lab measured data point plots. Such regression lines only pass through perhaps one or two hard data points (among many) as if by accident, and may well in fact pass through zero real data points. Thus if one is to call the likes of such regressions math model reduced formula output "reality", it must be by a serious stretch of the imagination.

And even if one is to go by models built upon A.J.'s carefully considered mathematical formulas, one would need to do detailed titration analysis upon each and every malt within a recipes grist in order to permit such precision in mathematics to reflect reality when attributed to ones own brew-day efforts. And when one replaces a malt, one must test again anew. Even letting a malt age on the shelf between brewing sessions may result in changes within its nature.

So in the end much of what is math modeled to be reality is hardly going to be reflected within ones typical brew day reality at all. Be it purely empirical as to its math modeling, or a quasi-empirical blend of hard science and pure empiricism, or rooted 100% in hard science.

And when I find it within my means to modify 'Mash Made Easy' to more closely reflect the strict math modeled output of one whom I admire as a genius, I make such modifications, as witnessed within this threads inspiration for my release of version 1.50. Perhaps the core simplicity of MME permits me to more rapidly respond and make adjustments to it than for far more complex projects. And the more complex it is, the more there is the potential for rather serious coding error which will be reflected in dubious and highly questionable output, such as has been being discussed within this thread for some very popular mash pH assistant software.

 

[ajdelange]

AJ I must be entering something incorrectly. Trying this in 4 different spreadsheets I am not seeing the same results. I see the pH values either decreasing slightly of staying the same when adding 10, 20 or 30 gallons of water.

You are assuming that one or more of those spreadsheets may be handling the chemistry correctly. DI water has, theoretically, a pH of 7 and an alkalinity of 0.002 mEq/L relative to the malt's DI mash pH. Thus when you add water to this malt you are adding a base to it and the pH is going to go up - but not by much. The spreadsheets that show 0 change don't fully implement the chemistry (i.e. ignore the alkalinity of water) or lose the subtle pH change to rounding and there is nothing wrong with that. Those that show it going down are simply wrong.

I remembered something from years ago to the effect that if you hit ctrl-` on an Excel spreadsheet it shows you what's in the cells so now I am really dangerous. Copy the following and paste it into column A of an empty Excel spreadsheet
Malt lbs
DI Water, gal
pHz

Malt kg
Water L

pHdi
a
b
c

Qmalt /kg
Qwater /L

Qmalt
Qwater
Qtotal

Now copy the following into column B
12.5
10
5.6227

=0.454*B1
=3.785*B2

5.6227
-40.69
14.821
-10.008

=B9*(B3-B8)+B10*(B3-B8)^2+B11*(B3-B8)^3
=1000*(10^-B3 - 10^(B3-14))

=B13*B5
=B14*B6
=B16+B17

You should now have a spreadheet that looks like this

In the first three rows of column B you enter a quantity of malt in pounds water in gallons and a trial pH. 5.6227 is the DI mash pH of Weyermann's pils referred to room temperature.

The formulas in rows 5 and 6 convert pounds and gallons into kg and liters. It's way easier to work these problems in metric. Rows 8 - 11 contain the data characterizing the malt. In row 13 the formula calculated the charge on the malt at pHz relative to what it is at pHDi. When you change the pH of a malt from its natural pH (pHDi) to some other pH (pHz < pHDI) its electrical charge changes and it takes protons to do that. Qmalt/kg tells you what the charge change is at pHz relative to pHDI. If pHz = pHDI, as it does art this point, obviously that number is 0.

The formula in row 14 does the same for 1 L of DI water i.e. tells what the charge on it is relative to what it is at pH 7 (where it is 0). This is the number of protons that would have to be supplied to get pure water to pHz.

In rows 16 and 17 the charge changes per kg and liter are multiplied by the kg and liters and added together in row 18 to give the total charge change for this 'mash'. B18 shows a charge change of 0.09 mEq for this mash at pHz = 5.6227. But that's impossible. When you add water to malt no charge change takes place so 5.6227 must not be the correct pHz. We need to find the pHz that brings cell B18 to 0. That value is pHz = 5.623089779 , slightly higher than pHDi. We have added a (very weak) base, water, to a malt and the pH of the mix is higher than the intrinsic pH of the malt. No surprise there. So how did we get 5.623089779? We used the Excel Soilver tool instructing it to set B18 to 0 by changing B3. It got B18 down to
1.6987E-11 which is close enough for government work.

In the following image I've added two columns for 20 and 30 gallons of water.

You can see from them that the pH rises a bit with each incremental addition. The cause of this is that more protons have to go to the additional water thus taking more from the malt resulting in higher pH, if only slightly. Note that the shifts here are an order of magnitude smaller than the shifts in the previous post. This lead me to find an error (a subtle one but an error nevertheless) in my larger spreadsheet and for that I owe you guys thanks for focusing me on this question!

 

[ScrewyBrewer]

Thank you for posting AJ. I recreated your example spreadsheet. And honestly if you don't mind wondering how to use it to duplicate your scenario?

 

[ajdelange]

Hey, I'm no genius. Just ask my wife.

Believe me or not this stuff is really simple. You all have focused me on it recently and the simplicity is more apparent than ever. I put up No. 82 to point out the absurdity of the notion that the pH changes proportionally with the mash water volume but No. 88 is there to show how simple it is to calculate these things, down to the tiniest of the minutiae, using the charge method. There are only 5 cells that actually do anything other than take input data and convert English to metric and of those all the heavy lifting is done in 2 (B13 and B14).

You can solve seemingly very subtle problems just by calculating the difference in charge on all the items in a mash (malt, water, cabo in the water, added acids, acid bases) at the pH at which the item is given to you and the pH you want. Those charges are as simple to calculate as the charges illustrated in the spreadsheet of No. 86. The model for water alkalinity is being illustrated (with another spreadsheet) in another thread at https://www.homebrewtalk.com/forum/threads/mixing-2-known-water-sources-basic-math-and-beersmith-question.651939/