The worlds easiest mash pH adjustment assistant method?

[Silver_Is_Money]

Some stuff I yanked straight out of Mash Made Easy version 9.20, as anyone can easily do since most of it is available on the opening screen for the case when grist weight is set to 1 Kg. and minerals are all set to zero. No reason to hide it when anyone with MME 9.20 has open access to it. The only calculated column is the "buffer value when stripped of kludge" column.

Perhaps if I attempt an upgrade to MME v_9.20 I will eliminate its internal application of the kludge.

NOTE: All of this data was gleaned from a single pass through MME without double checking any of it. Hope I didn't have wandering eyes or fat fingers, etc...

 

[Silver_Is_Money]

If you confidently and fully understand all of the critical safety issues and dangers and proper procedures involved, then the following are means whereby to make 1L quantities of 0.1N titrants (acid and base):

1) 8.3 mL of Concentrated 37% HCl when made up to 1L with DI or distilled water = 0.1N Acid

2) 4.00 grams of pure crystalline NaOH (sodium hydroxide) when made up to 1L with DI or distilled water = 0.1N Base or Caustic

 

[Big Monk]

If you confidently and fully understand all of the critical safety issues and dangers and proper procedures involved, then the following are means whereby to make 1L quantities of 0.1N titrants (acid and base):

1) 8.3 mL of Concentrated 37% HCl when made up to 1L with DI or distilled water = 0.1N Acid

2) 4.00 grams of pure crystalline NaOH (sodium hydroxide) when made up to 1L with DI or distilled water = 0.1N Base or Caustic

One thing I was trying to get across before Larry was that i'm not sure the average brewer would even have to titrate the malt. I think the data set that exists is a sufficient jumping off point, such that you could use the values for a Euro Pilsner and tweak them on subsequent batches to have mEq values for that malt that exceed the effectiveness of color based acidity, for example, by a huge margin.

Contrary to what some might think, I am all for making this process easier on folks and frankly, i think people will have a much harder time getting titrations correct than just revising existing co-efficient sets to match the "field". With that said, people would want to make sure the rest of the constituents parts (measurement devices, acid amounts, grain weights, water composition) were well sorted before they could reliably single out malt as a variable to play with.

 

[Silver_Is_Money]

One means to quantify the kludge factor multiplier (or at least the way I quantified it):

If it is presumed that a typical base malts buffering value is ~45.5 mEq/Kg_pH, as per a published peer reviewed paper by D.M. Riffe, then the kludge represents the means to normalize 45.5 mEq/Kg_pH to Kolbach's presumption of 32 mEq/Kg_pH for a typical base malt.

32/45.5 = 0.7033

MME comes pre-set to 0.7000 for its kludge factor, but you are free to tweak it to 0.7033 (or any value between 0.60 and 0.80)

0.7000/0.7033 x 32 = 31.85 (which is right close to the nominal mid-range of the base malt buffer values seen in my post #91 above.

 

[Big Monk]

One means to quantify the kludge factor multiplier (or at least the way I quantified it):

If it is presumed that a typical base malts buffering value is ~45.5 mEq/Kg_pH, as per a published peer reviewed paper by D.M. Riffe, then the kludge represents the means to normalize 45.5 mEq/Kg_pH to Kolbach's presumption of 32 mEq/Kg_pH for a typical base malt.

32/45.5 = 0.7033

MME comes pre-set to 0.7000 for its kludge factor, but you are free to tweak it to 0.7033 (or any value between 0.60 and 0.80)

0.7000/0.7033 x 32 = 31.85 (which is right close to the nominal mid-range of the base malt buffer values seen in my post #91 above.

I still don't see a need for this kludge. It seems to treat a symptom rather than a problem.

 

[Silver_Is_Money]

I still don't see a need for this kludge. It seems to treat a symptom rather than a problem.

Without it the acid required to move a base malt (etc...) from pHDI to target pH proves to be overstated by about 30%, Unless your internally utilized buffering values are 30% lower than published values which I have free access to.

For example: Without the applied kludge, where MME says 'hypothetically' to add ~4 mL of 88% Lactic Acid, it would instead say to add ~5.7 mL.

 

[Big Monk]

Without it the acid required to move a base malt (etc...) from pHDI to target pH proves to be overstated by about 30%, Unless your internally utilized buffering values are 30% lower than published values which I have free access to.

For example: Without the applied kludge, where MME says 'hypothetically' to add ~4 mL of 88% Lactic Acid, it would instead say to add ~5.7 mL.

I guess I'm not following. Overstated with respect to what? It could also be your pH DI is off, i.e. low.

 

[Silver_Is_Money]

I guess I'm not following. Overstated with respect to what?

To what works a bit better for me (at least), here in my back yard or garage based home brewing world. As stated earlier I believe it is potentially related to mash efficiency in some means. And with my crude equipment my embarrassing efficiency is nothing to write home about. My efficiency is likely nothing near what can be achieved in a lab setting within a Congress Mash.

Don't quote me on this, but I believe D.M. Riffe is applying the kludge in the range of 0.65. He initially gauged it at around 0.6.

 

[Silver_Is_Money]

If you can't squeeze all of the acid from the grist into the Wort during the mash, just as for if you can't squeeze out all of the sugars, then it goes without saying that less acid/base adjustment to the Wort pH at some level is called for. That is how I see it (I.E, the kludge) at least. I certainly may be all wet in my reasoning here though. As I say, intuition often makes for bad science, and this is admittedly my intuition.

 

[Big Monk]

To what works a bit better for me (at least), here in my back yard or garage based home brewing world. As stated earlier I believe it is potentially related to mash efficiency in some means. And with my crude equipment my embarrassing efficiency is nothing to write home about. My efficiency is likely nothing near what can be achieved in a lab setting within a Congress Mash.

Don't quote me on this, but I believe D.M. Riffe is applying the kludge in the range of 0.65. He initially gauged it at around 0.6.

So that definitely gives more insight. My testers are drawn from a pool of people with Extraction Efficiency upwards of 95% and Mash Efficiency exceeding 80%, including those who are performing no-sparge batches as a general rule. This kludge is not required in my experience. I would suspect those getting good efficiency and highly efficient mixing would set that value in your sheet or Riffe's to 100%.

In any event, insufficient extraction and less than stellar mixing of the mash are symptoms of other, non-pH related issues.

 

[Silver_Is_Money]

So that definitely gives more insight. My testers are drawn from a pool of people with Extraction Efficiency upwards of 95% and Mash Efficiency exceeding 80%, including those who are performing no-sparge batches as a general rule. This kludge is not required in my experience. I would suspect those getting good efficiency and highly efficient mixing would set that value in your sheet or Riffe's to 100%.

In any event, insufficient extraction and less than stellar mixing of the mash are symptoms of other, non-pH related issues.

Agreed! Via "Data Validity" criteria, I have it maxed at 0.8 presently. Perhaps I need to open it up to 1.00.

 

[Silver_Is_Money]

At this juncture I've literally poured out the soul of both my entire thinking as to my dabbling into SRM based, and as to a fair portion of the inner workings of MME. It is often said to be dangerous when one opens ones soul to scrutiny, but I'm in agreement with finding improvement where it can be found also, and I'm not getting any younger, or healthier. And another of my sayings is: "You can't tell how to get where you want to go if you don't first know where you're at."

 

[VikeMan]

"You can't tell how to get where you want to go if you don't first know where you're at."

"And if you don't know where you're going
Any road will take you there"
--- George Harrison

 

[Silver_Is_Money]

"And if you don't know where you're going
Any road will take you there"
--- George Harrison

Something akin to that approach worked for the SRM method.

 

[Silver_Is_Money]

For instance, we get the following from A.J.:

dQ (mEq/kg) = a1 * (pHz - pHDI) + a2 * (pHz - pHDI) ^ 2 + a3 * (pHz - pHDI) ^ 3

where a1, a2 and a3 are titration co-efficients that describe the specific malt's mEq/kg properties in a mashing system. Technically you could go to the aN co-efficient with incremental increases in accuracy but more than likely a1 and a2 are sufficient.

I'm not faulting this, your herculean effort to sustain and promote the excellent work of AJ. But in the end this must be accepted as merely another math model, albeit of an exponential curve. There is no mystical proton balancing magic in it at the degree that I sometimes perceive you may understand it as having, such that it actually achieves proton balancing perfection (which it does not, being only a modeled attempt at generally mimicking real world observation, just as for any other math model). It is in the end merely a math modeled attempt at mimicking titration effects which I have already admitted are not quite linear over vast scales of titration degree, albeit are (IMHO) sufficiently linear within the region of pH_T (what this equation calls pHz). What I'm calling pH_M, this model calls pHDI. What I'm calling mEq_Grist, this model calls dQ. Variable naming within formulas is merely arbitrary and at the discretion of the formula generator, so no mystical magic resides there either. And as AJ stated, extra titration coefficients tossed at this beyond the arbitrary 3 he chose will continue to incrementally add more potential precision, but in the end never quite achieve what is actually unachievable perfection. The key here (the short version) being that any math model will never be perfect no matter how many atom bombs (coefficients) one applies to it. Whereby in championing it (which again I deeply admire) I perceive that you place a level of faith in its perfection that is not truly warranted. And this leads to the crux of the matter: How much precision is warranted? As I've asked above somewhere, what improvement in flavor or stability does targeting 5.40 pH and hitting 5.41 vs 5.44 bring to the actual beer, when 5.4 itself is nothing more than an entirely arbitrary target, and little effort at even the commercial level has been placed in justifying it (as well as the entire mash pH targeting issue) other than via unattested as to its veracity "circular reasoning", as attested by Bamforth.

As I said, the greater degree to which one titrates, the more the extant non-linearity appears. 3 titrations reveal said non-linearity, and justify a fit "attempt" via an exponential equation as opposed to a linear equation. But even (to my knowledge) D.M. Riffe has found the small potential gain in pH target hitting precision to be simply not worth the effort, and he has openly stated so on this forum. You do also admit to this very same thing for most malts, albeit that you preface that for acidulated malt and Munich malts it models (for you) a bit better. Why continue to titrate to pH 4.3 or lower or pH 7 or higher when the target itself is 5.4? Why not simply titrate within the proximity region of the intended target?

The general audience needs to know these things. AJ is a blessed giant among giants, but he is not a god. And in my opinion he is not at nearly the gravitas level of Bamforth, whom is also not a god.

 

[Silver_Is_Money]

In response to a forum members proclamation that "The best professional breweries check PH", AJ deLange replied:

That's arguable. When addressing professional brewers on the subject I ask "How many of you check pH and have never had more than perhaps a third respond that they do. I can't attest as to whether this group contained the best brewers in the room. I have also had professional brewers tell me "You home brewers take this stuff much more seriously than we do."

Here's the link:
https://www.homebrewtalk.com/threads/ph-how-important-is-adjusting-for-ph.655119/post-8385019
And a bit further on in the very same thread we read this from another obviously knowledgeable forum member:

I've spent a career researching enzymes similar to barley amylases and enzymes in this class have broad pH optima. The barley amylases retain >90% of their activity over a pH range of ~4.5 - 6.5, so the claims of efficiency and FG changing with mash pH have never computed for me. The studies I have seen on this don't statistically back up the claims either. I thought, however, that perhaps the favours of the beers may be affected by the mash pH and that is why many people seem to agonize over pH so much. However, when I have looked into this, the sensory data I have seen (not much in truth) is pretty weak and did not convincingly link mash pH to strong impacts on flavour.

 

[Silver_Is_Money]

Looking at this another way:

Recognizing the obvious non-linearity of titration "curves" (inherent in why they are defined as curves) over broad pH expanses, MME intentionally restricts targeted pH to 5.1-5.8. If one had a true desire to adjust a mash to (for example) pH 4 as the target, AJ's exponential curve fit would undeniably yield an appreciably better (though not perfect) acid adjustment addition answer. But any difference in the answer at pH 5.4 as the target is vastly more impacted by ones initial choices of buffering factor and pHDI valuations for each of the individual grist components within a recipe than for ones choice to presume conformance to linearity (all that can be presumed from but a single titration point) or non-linearity (as can emerge only from multiple titration points) within the general vicinity of pH 5.4. The greatest errors lie within the two highlighted variable valuation presumptions.

 

[Silver_Is_Money]

They say a picture is much better than a thousand words, so (being that it is in my nature) I will add a thousand words to this anyway...

I copied the AJ chart seen below from the 'Water' book by Palmer/Kaminski. It shows that AJ says we need to add 40-32 = 8 mEq/Kg of acid to go from 5.75 pHDI to our target of 5.4 pH via his excellent exponential curve fit model. It further shows that per the linear fit model we need to add 43.1 - 32 = 11.1 mEq/Kg to move from 5.75 pHDI to our target of 5.40 pH. A whopping 38.8% overshoot in acid. But it also shows that (due to buffering and the log base 10 nature of pH) by adding this massive overshoot we (per the presumption of perfection for AJ's chart) will hit 5.32 pH instead. An error of 5.4/5.32 = 1.5%.

Note that the linear method (single titration point model) line I added comes from my hypothetical titration of a 32 mEq/Kg_ph5.4 base malt, wherein we added 1 mEq of acid to accomplish moving from 5.75 pH to 5.15 pH for the case of 50 grams of this malt. 1 kg. as seen for this chart should require 1000g/50g * 1 mEq = 20 mEq's, as is fully confirmed by moving from 32 to 52 mEq's on the chart. Thus AJ's malt and my hypothetical malt are for all practical purposes identical, indicating a perfect fit of this chart whereby to overlay upon it our hypothetical malt titration. Short version: This shows that I'm justified in my linear line positioning.

Bottom line is a relatively minor 1.5% pH projection error for the simplistic linear presumption model. And it just so happens that this also represents (by chance due to 5.4 being close to midway between 5.75 and 5.15 pH) nearly the maximum error we can expect to receive from the presumption of linearity that comes naturally from but a a single titration point. If we had been targeting a different pH than 5.4 our error would potentially be less. And this confirms my admonition that a single titration point should not be reconed via the addition of an excessive mEq addition of acid.

 

[Silver_Is_Money]

Flash thought: Could it be that the above 38.8% overshoot is the main if not only reason behind the logic of D.M. Riffe's correction factor (formerly called the kludge, and before that, the fudge factor)?

Is it now to be considered a nominalized corrector whereby to bring linear presumption in line with exponentials better fit to reality? Hmmm???

That would about fully explain why Big Monk does not find a need for it, whereas linear based math models do.

Thinking! Thinking! Learning! Learning! Perhaps.... (as intuition often leads to bad science)

Could just as well be coincidence. After all, correlation does not imply causation. Wake up Larry!!! (OK, I'm awake now, 3 edits later)

 

[Big Monk]

Whereby in championing it (which again I deeply admire) I perceive that you place a level of faith in its perfection that is not truly warranted. And this leads to the crux of the matter: How much precision is warranted?

A few thoughts:

1.) Nowhere have I ever said it's perfect. For a long time, we had no other option but color based acidity proxies, i.e. we had no way to model, directly, the acidity of the malt based on titration. The point? There was only one game in town and now there is not. That's all. I'm all in for progress.

2.) As far as precision is concerned, A.J. has always said, and i agree, that we should be shooting for precision in all other facets EXCEPT malt because we really can't expect perfection and precision with an agricultural product, especially when we consider the work to titrate it and the potential error that brings forward. The point? A.J. wanted shortcuts associated with the other parameters to be a thing of the past, i.e. pH dependence, acid calcs, source water, etc. and their associated kludges.

So, I see what you are saying but I don't agree with you when you say that I think the malt model is perfect. Far from it. It is a progression that moves away from color based malt acidity, which in itself was a kludge.

 

[Silver_Is_Money]

A few thoughts:

1.) Nowhere have I ever said it's perfect. For a long time, we had no other option but color based acidity proxies, i.e. we had no way to model, directly, the acidity of the malt based on titration. The point? There was only one game in town and now there is not. That's all. I'm all in for progress.

2.) As far as precision is concerned, A.J. has always said, and i agree, that we should be shooting for precision in all other facets EXCEPT malt because we really can't expect perfection and precision with an agricultural product, especially when we consider the work to titrate it and the potential error that brings forward. The point? A.J. wanted shortcuts associated with the other parameters to be a thing of the past, i.e. pH dependence, acid calcs, source water, etc. and their associated kludges.

So, I see what you are saying but I don't agree with you when you say that I think the malt model is perfect. Far from it. It is a progression that moves away from color based malt acidity, which in itself was a kludge.

I'm glad my presumption was a misconception. Funny how all of us are capable of misconceiving the intent and motivation of others. And generally do.

 

[Big Monk]

The major thing here is that all our sheets should have agreement with respect to water composition, acid amounts, etc. I am obviously an outlier because of my malt modelling, although Riffe's stuff is in the sam wheelhouse as me now for everything except Sauermalz. For Sauermalz, I am truly alone, as I model that as a malt.

So malt modelling is really what defines all our individual programs and should really be the only difference in my opinion between the various programs.

 

[Silver_Is_Money]

Agree!

I just had a new thought. If Congress Mash titrations were all intentionally undertaken via the single titration point method whereby to hit a measured 5.4 pH via the addition of 0.1N acid or caustic, then to a target of pH 5.4 (the most popular overall target) the linear method should exhibit zero error, presuming that a Congress Mash actually scales perfectly to the average hombrewers batch size level and process. A big presumption perhaps.

This would mean titrating while monitoring pH on the fly and simultaneously. Auto-titrators with built in pH metering capability come to mind here. Ditto a temperature bath to counter the tendency of exotherm during titration and stirring.

 

[Silver_Is_Money]

Buffer question for the day: If (as I suspect) most of the buffering values found within published literature were derived from single point titrations, how can they be made to properly function whereas to yield valid output within a three titration system.?

 

[Lupulus]

The latest posts are a very interesting read. Thanks for taking the time!
Please only read this as a helpful comment.
The difference between a pH of 5.4 and 5.32 is approx 20%
Useful memory tricks...
0.3 pH difference is approx 2x
0.5 pH difference is 3.16x (I use Pi to remember)
0.7 pH difference is approx 5x
1 pH difference is 10x

 

[Big Monk]

Buffer question for the day: If (as I suspect) most of the buffering values found within published literature were derived from single point titrations, how can they be made to properly function whereas to yield valid output within a three titration system.?

In descending order, here are the data point sets I know with their originator and number of titration points:

deLange = 3 point
Walts = 2 Point
Bies = 1 Point
Guerts = 1 Point
Troester = 1 Point
Riffe = 1 Point

I don't have the answer to your question. I took all this data and made a master list of "Malt Classes" that combined some of the data into a single set, some of which combined data sets from a few similar malts to expand some from single to dual point or dual to three point sets. Obviously single point or double point titration data can be plugged into the 3 term equation of A.J.'s just fine. I believe Riffe's work involved fitting the deLange and Walts data to a single point around a1 and then normalizing all the data. I used raw data with heavy emphasis on the deLange and Walts data to try and expand single point sets to dual or three wherever possible.

I expect Riffe may be more technically sound here but I tried to use common sense wherever I could.

Keep in mind that the equation will simply ignore any of the polynomial terms not used for sets that are not full 3 point. As to the accuracy, obviously if you plug a single or dual point set into the 3 term polynomial equation, it will yield different results in terms of malt dQ (mEq/kg).

 

[Silver_Is_Money]

The latest posts are a very interesting read. Thanks for taking the time!
Please only read this as a helpful comment.
The difference between a pH of 5.4 and 5.32 is approx 20%
Useful memory tricks...
0.3 pH difference is approx 2x
0.5 pH difference is 3.16x (I use Pi to remember)
0.7 pH difference is approx 5x
1 pH difference is 10x

Completely true on the basis of free H+ ions. The very same issue as I was discussing within post #16 in fact.

10^-5.32/10^-5.4=1.2023, or 20.23% more free protons floating around, which is precisely the reason why a pH meter would read it at 5.32 pH instead of 5.40 pH. But 5.2 pH to 5.6 pH at room temperature during the mash is accepted as being just fine, so we are nowhere near leaving the ballpark. It's a very big ballpark. And logarithms of base 10 are quite thankfully our friend here.

 

[Big Monk]

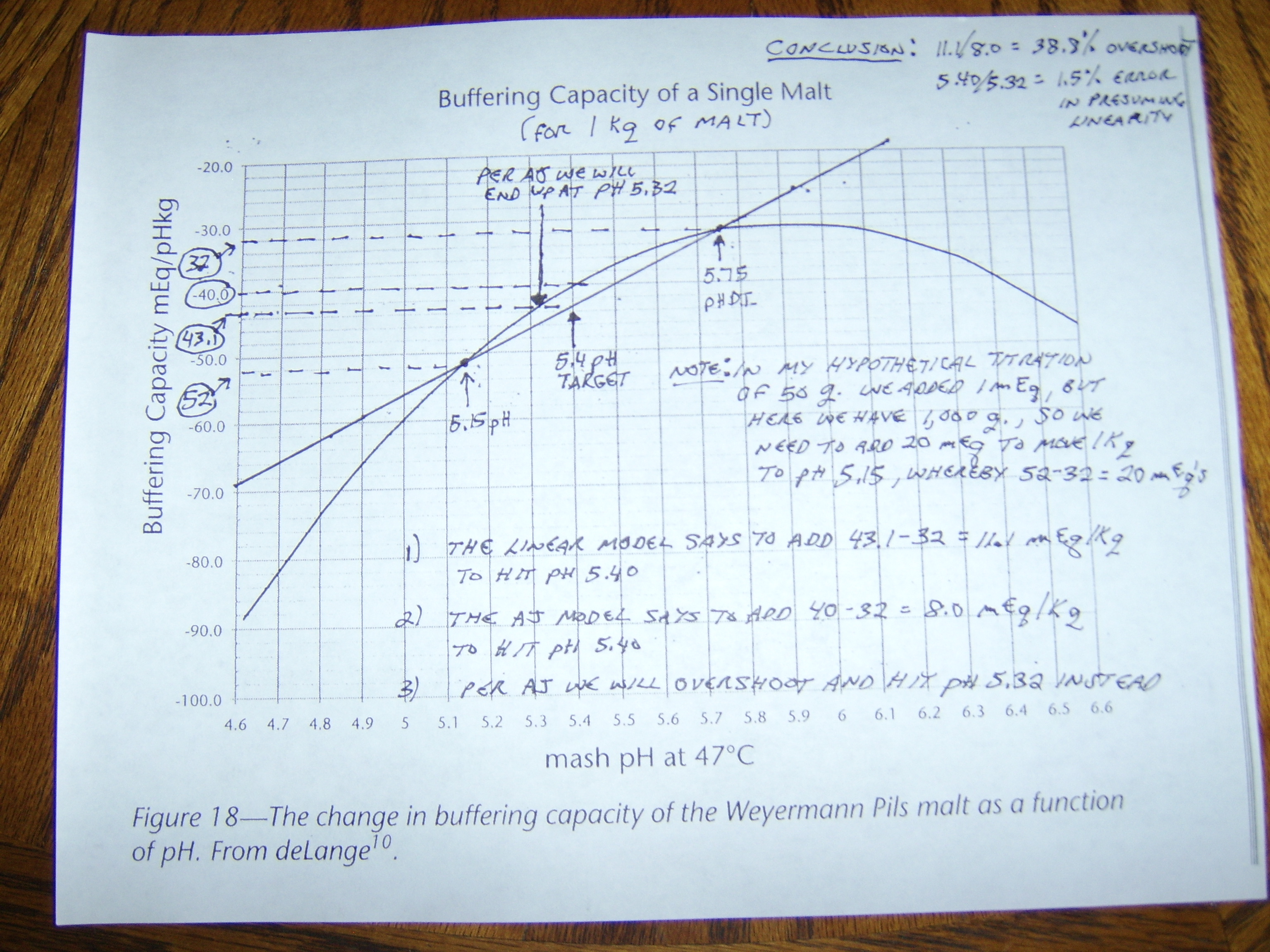
I got to thinking about something and ran a few tests. The crown jewel for me in the malt data that I have is A.J.'s Weyermann Floor Pils:

It has all 3 terms and a pH DI that corresponds to past and present pH DI values from lot analysis from Weyermann. I merely took it, changed the pH DI to my Weyermann average from my lot analysis data bank, checked the 2019 analysis values across their pilsner range, and used it for my European Pilsner malt class:

I want to see the effect of simply taking this and removing a3 and a2 sequentially. My thought being that anyone can stop at any point in the process of tritrating malt and simply not go beyond a1.

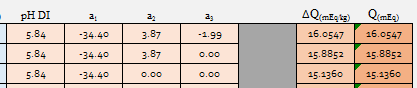
I used the "Custom Malt Parameters" slots and just forced it to be a dual and single point set:

I set source minerals to zero with Alkalinity set to 1.58 mg/l as CaCO3, remembering that value was what A.J. always spec'd for DI water. 1 Kg each of European Pilsner, Custom 1 and Custom 2 yields:

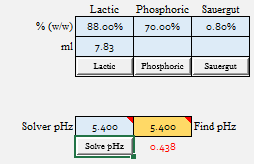
After just whipping up some reasonable batch parameters (32 l strike volume, 5.67 kg of malt, DI water, no added minerals for simplicity), I ran each malt to see what value of 88% Lactic Acid it would take to go from Grist pH to 5.4:

European Pilsner (3 Term):	European Pilsner (2 Term):	European Pilsner (1 Term):
Grist pH = 5.838	Grist pH = 5.838	Grist pH = 5.838
Lactic Acid to 5.4 = 7.91 ml	Lactic Acid to 5.4 = 7.83 ml	Lactic Acid to 5.4 = 7.46 ml

I'm not exactly sure what my point is other than if we have a reliable data set for a malt, that makes sense from a practical standpoint, we can show that we really do not seem to introduce much error in the amount of acid required to acidify the batch from assuming it to be linear.

The rub here is that we can only test this if we have a 3 point data set. I know that Riffe was confident in the point I just made when he normalized 3 point data sets to linear, as it agreed pretty much with what I have shown. However, we can never really be sure that single titration point data is as "accurate" for crystal mats, roasted malts, adjuncts, etc. because we don't have any 2 or 3 point data sets to compare them to.

 

[Silver_Is_Money]

I'm presently working on version 9.30 of MME, and I believe I will take Big Monk's advice and default the buffer multiplier (correction factor, kludge) therein to 1.00, whereby its impact is zero. It will still be there just in case it is clearly proven to have merit, whereby it can be set by the user to values spanning anywhere between 0.6 (maximum effect) and 1.0 (no effect).

Among other changes, 9.30 eliminates the base malt drop down selector cell/switch and moves all of the base malt selection choices which formerly resided there over to the standard grist component 'drop down' entry column. It also assigns individual buffering values to each type of base malt, instead of ganging them under a single buffer value. In addition it splits Biscuit, Munich, and Aromatic into their own independent categories. A huge overall change. I could use a couple Beta testers. PM me if interested in kicking the tires.

 

[Silver_Is_Money]

I would like to see what a 3 point titration curve for a malt with a pHDI of less than the 5.4 target pH looks like. It may prove to be the case that for the single titration buffer calculating method, any malt that is acidic with respect to target pH gets over corrected for as well, but this time in the opposite 'sign' direction, negating some of the acid over-addition error induced by a grists base malt(s) and other of malts with > 5.4 pHDI. This potentially beneficial error in the opposite direction would happen for those grists which contain acidic malts such as Melanoidin, Caramel/Crystal, or Deep Roasted, etc.... So for many grists the error may well be less than the calculated 0.08 pH points witnessed for the charted example seen above.