Test Mash

[dmcmillen]

I would like to do a test mash to verify and adjust as necessary the water additions suggested by Bru'n Water so that I make sure I hit my desired mash pH. I am looking for some ideas on the best way to actually do the test mash. I obviously can't do with my brew dauy equipment. I'm thinking of using a pan to hold the grist & mash water immersed in a larger pan of water on the stove that can be heated. My questions are:

• What equipment do folks use to do a test mash? I'm sure there's more that one way to skin the cat.
  
• How small should I scale my grist bill down to? A pound (or less??)?
• Do I have to duplicate my brew day mash; i.e., if calls for 155 for 60 mins is that what I need to do for the test/mini mash or is say 30 mins ok and do I have to hit my 155? How important is the time and temp for the test?
  
• I am assuming I scale the Bru'n Water suggested treatments down to the test mash. Could just create a Bru'n Water test mash profile with the grain and water amts to get the additions.
• How to calculate the addition amts to change +/- .1 acid or alkali? I have been altering the adjustments in Bru'n Water till I get the swing I want and noting the amount of the addition that caused the .1 swing. This varies for every recipe.
• Should I make additions to the test mash until I hit the desired pH or just extrapolate to the mash day recipe.

Appreciate some direction here.

David

 

[jekeane]

what about Brun or the mash ph are you trying to test exactly? Whether or not it's accurate?

I can say from my experience using both ro and house water that it is rarely ever off. If it is off it is no more than .1 which is more likely .05 ish due to being on the edge of range. I test most mashes with my pocket pro+ and it's to the point that I don't feel its necessary to test when I use ro.

 

[dmcmillen]

So far, with my meter (Milwaukee 102) calibrated and confirmed stabilized, I am not coming close to the pH that I am expecting to hit from Bru'n water. So far I have been off as much as .2 to .3 more than I would expect. It was suggested that I should perform a test mash. So far I have not had a brew that required DI water (since trying to manage pH), so I am using my whole house filtered water that was tested by Ward labs and is entered into Brun. Grains are entered into Brun correctly. I would be really happy to get within .05. I follow AJ's procedures for taking and testing the sample. I'm pretty much scratching my head.

 

[mongoose33]

So far, with my meter (Milwaukee 102) calibrated and confirmed stabilized, I am not coming close to the pH that I am expecting to hit from Bru'n water. So far I have been off as much as .2 to .3 more than I would expect. It was suggested that I should perform a test mash. So far I have not had a brew that required DI water (since trying to manage pH), so I am using my whole house filtered water that was tested by Ward labs and is entered into Brun. Grains are entered into Brun correctly. I would be really happy to get within .05. I follow AJ's procedures for taking and testing the sample. I'm pretty much scratching my head.

Are you cooling the sample to room temp before testing for pH?

 

[ajdelange]

I can say from my experience using both ro and house water that it is rarely ever off. If it is off it is no more than .1 which is more likely .05 ish due to being on the edge of range.

As Bru'n Water (nor any other spreadsheet) is capable of this level of accuracy (.1 yes, 0.05 no) this only says you are not doing the measurements properly. The most likely problem is Confirmation Bias.

I test most mashes with my pocket pro+ and it's to the point that I don't feel its necessary to test when I use ro.

Now if you brew the same beer over and over again using RO water with the same treatment and the same malts every time it is likely that you will have tuned the process to hit the pH ±0.05 every time to the point where you feel it isn't necessary to check each mash. But if you see error of less than 0.05 for every new beer you run through a spreadsheet you are probably not doing the measurement right. Yes, it is possible to flip a coin 40 times in a row and get heads each time but the probability that this will happen is tiny (odds are a million to one). Or, put another way, if it seems to good to be true, it probably is. dmcmillen's results are more typical.

 

[dmcmillen]

Yes. I have been pretty rigorous in following AJs procedures.

 

[ajdelange]

• What equipment do folks use to do a test mash? I'm sure there's more that one way to skin the cat.

• 
  
  
  Lots of possibilities here. Anything that holds a pound or so of grist. A small saucepan that fits into a larger one filled with warm water would do.
  
  
  

• How small should I scale my grist bill down to? A pound (or less??)?

Yes, that's a pretty good size

• Do I have to duplicate my brew day mash; i.e., if calls for 155 for 60 mins is that what I need to do for the test/mini mash or is say 30 mins ok and do I have to hit my 155? How important is the time and temp for the test?

Try to get as close to your strike temperature as possible. If you strike at 155 then try to get the larger volume of water to that temperature and pre warm the grains by sticking the container holding them in that water bath for some time. Then add water at 155 to the grains. Try to hold the temperature near this for at least 20 min and measure the pH then (after cooling to room temperature)

• I am assuming I scale the Bru'n Water suggested treatments down to the test mash. Could just create a Bru'n Water test mash profile with the grain and water amts to get the additions.

Yes, scale down from the quantities to be used at mashing.

• How to calculate the addition amts to change +/- .1 acid or alkali? I have been altering the adjustments in Bru'n Water till I get the swing I want and noting the amount of the addition that caused the .1 swing. This varies for every recipe.

Grains have buffering of about 40 mEq/kg•pH which you can use to estimate how much acid is needed for a pH shift. As not all grains have this buffering you won't get the acid adjustment exactly correct but over the small pH region of interest you can interpolate between the pH readings you got with the original and corrected acid additions.

• Should I make additions to the test mash until I hit the desired pH or just extrapolate to the mash day recipe.

I'd say that depends on how close you get. If quite close just use the amount you used in the test. Ideally you would make 2 test mashes and interpolate/extrapolate from their results. Or you could extrapolate using the 40 mEq/kg•pH result but to do this you would need to know the strength of the acid. With two test mashes you can interpolate/extrapolate in mL.

 

[dmcmillen]

AJ, thanks for the info on the mash technique. It's been a long, long time since I've had a chemistry class. I know that mEq stands for milliequivalents but 40 mEq of what per kg of what (assume grain here) and is that times the measured pH? You said I can use that to determine how much acid is needed for a pH shift. How do I do that?

You're also talking about calculating how much acid but what if I need to raise the pH if I'm too acidic. If I'm at 5.1 and need to be at 5.3 I probably need to know how much bicarbonate to add to raise the pH by that amount. Same problem is how to calculate that. Obviously Bru'n Water is calculating all of that behind the scenes with the water adjustments which is why I have been using Brun for each recipe to pre-calculate the additions that would add or subtract .1.

Hate to show my ignorance here but could you help me understand how to calculate the quantity of addition that will cause the desired swing. I am fine with the math. I appreciate your patience and help.

 

[ajdelange]

.

 

[dmcmillen]

AJ, your previous post was empty. I have a layman's understanding of the high level concepts here. I believe that the buffering capacity of a solution is the quantity of a acid or base that will change the pH (change 1 liter of solution by 1 pH unit). I suppose there is an minimum amount required to overcome the tendency to remain stable. My problem, of course, is understanding how to calculate the amount to affect the change I desire because the buffering units don't mean anything to me in terms of calculating quantity or knowing what pH swing that quantity will produce. As I watch more videos of home brewers adjusting their pH, most I see just add small amts of acid or base until they get the result they want.

 

[ajdelange]

Yes, aware that my last post is empty. Half way through typing it it automatically posted it so I edited it to a dot and posted that and then edited the dot with where I was when it auto posted and well into that editing it (the server) just wiped everything out. I wasn't in the mood to retype everything last night and so left it as is. Today you are going to get a better answer than what got destroyed.

AJ, thanks for the info on the mash technique. It's been a long, long time since I've had a chemistry class. I know that mEq stands for milliequivalents but 40 mEq of what per kg of what (assume grain here) and is that times the measured pH?

A milliequivalent is 1/1000 mole of charge. In this case the charge on a proton and by, implication, the number of protons required to be added to a mash in order to effect a desired pH shift. Buffering of 40 mEq/kg•pH means that if you want to shift the pH of a mash down by 0.1 pH unit you must add 0.1*40 mEq of protons for each kg of malt in the mash. Note that this only covers the mash. A bit of additional acid will be required to neutralize any alkalinity in the liquor but as the alkalinity is mostly gone by the time you approach mash pH little error is incurred by ignoring it.

You said I can use that to determine how much acid is needed for a pH shift. How do I do that?

I think an example would be the best way to address this. Let us assume that we are going to brew with grist made up of 90% Weyermnann Pilsner malt and 10% Briess 20L Caramel malt and our water is at a pH of 8 and has alkalinity of 2 mEq/L which is 100 ppm as CaCO3. Alkalinity of 2 mEq/L means that when the analyst measured the water he had to add 2 mEq of protons (from some acid - usually sulfuric) to a liter of it to get its pH down to 4.5 which is the ISO standard value for the test. We want a mash pH of 5.4. We enter this data into some spreadsheet and it tells us that we need some amount of 88% lactic acid which is, at this desired mash pH about 11.5 N meaning that in acidifying to this pH each mL of it will deliver up 11.5 mEq of protons. Converting the spreadsheet recommendation to mEq and dividing by the total mass of the grains we find the acid recommendation to be 5 mEq/kg. We intend to mash with 2 liters of water per kg of malt (about a quart per pound) and so make a test mash with 900 grams of the pilsner malt, 100 grams of the caramel and 2 L of water (it could equally well be half this much of everything but having a kg of malt will make the math a little clearer later on). We check the pH of this test mash after 20 minutes and find the pH to be 5.52 which is 0.12 higher than we wanted and we clearly need more acid than the spreadsheet suggested. This is where the 40 comes in. We have to get pH down by 0.12 and know that malts have buffering of about this much so we calculate that 0.12*40 = 4.8 mEq more acid would get this test mash closer to target. We make another test mash using 5.0 + 4.8 = 9.8 mEq of acid and find the pH does indeed decrease to 5.42. This is definitely close enough for government work but being interested in what is happening here we calculate the ratio of the acid additions we made to the pH changes they caused. This gives us (9.8 - 5)/(5.52-5.42) = 48 mEq/kg•pH as the actual buffering of this mash which is appreciably greater than the 40 we assumed but, as the pH changes we are interested in are small, this 20% error in the estimated buffering does not make that much difference. It is now a simple matter to use the new buffering estimate to calculate how much more acid we need to get right to 5.4 and that is 0.02*48 = 0.96 mEq more for a total of 9.8 + 0.96 = 10.76 mEq. Since the test mash is 1 kg we could just multiply this new number by the total kg malt we intend to mash to get the amount of acid we need to brew with. There isn't much point in making a third test mash.

Note that we could come up with an estimate of the buffering by making the first test mash with no acid addition. Based on what we know about these malts it is expected that such a test mash would have a pH of 5.63. Then, comparing to a test mash with 5 mEq acid added we'd estimate the buffering as (5 - 0)/(5.63 - 5.52) = 45.4545 which isn't that much different from the 48 estimated from two acid containing test mashes. To get from pH 5.52 (test mash with 5 mEq/L) to the desired 5.4 would, using this buffering estimate, require 0.12*45.45 = 5.45 mEq more acid for a total of 5 + 5.45 = 10.45 which isn't that different from the 10.76 estimated with two acid using test mashes. The reason for the difference is that the buffering isn't constant. It varies with pH. The plot below shows what we have discussed so far in graphical terms

The non linearity is plain though it is not great. It is caused mostly by the Weyermanns malts and a bit by the remaining alkalinity. Some malts are more linear than this one and some less. Thus the closer to target pH you make the buffering estimate the more accurate it will be.

We have been casually talking about adding so many mEq/L protons so far but you usually don't buy acids labeled in strength expressed in mEq/mL proton content. The two acids home brewers use most often (phosphoric and lactic) have normalities (mEq protons per mL) that vary according to the target pH. As noted 88% lactic is 11.5 N at pH 5.45. 10% phosphoric is 1.09 N and 80% phosphoric 13.5N. Note that you don't have to do your buffering calculation in terms of mEq. You can do them in terms of mL of acid as well. The graph has a second vertical scale (at the right) in mL of 88% lactic acid.

You're also talking about calculating how much acid but what if I need to raise the pH if I'm too acidic. If I'm at 5.1 and need to be at 5.3 I probably need to know how much bicarbonate to add to raise the pH by that amount. Same problem is how to calculate that.

In order to answer this and continue to use the graph let us suppose that you made a test mash with no acid addition, observed the 5.63 pH and (not that you would ever want to do this) wanted pH 5.7. The graph says we need to get rid of 2.5 mEq of protons. We do this not by adding 2.5 mEq of anti-protons (that would be interesting - energy yield approximately equivalent to 40 tons of TNT) but by absorbing 2.5 mEq protons with a base. Each mmol of sodium bicarbonate absorbs 1 mEq of protons (at mash pH H+ +HCO3- --> CO2 + H2O) and so we would need to add 2.5 mmol of NaHCO3. As it's molecular weight is 84 mg/mmol we'd need 2.5*84 = 210 mg to raise a source water mash at pH 5.63 to 5.7.

 

[dmcmillen]

AJ, so sorry you had to input twice. Been burned enough that I've gotten where I copy long posts before submitting for that reason. I can't tell you how helpful this was. I have a much better understanding of how it works now. I really appreciate you taking the time to explain. Couple of quick questions.

Can I infer from above that if my Alkalinity from my water report is 98 ppm as CaCO3 then my alkalinity is 1.96 mEq/L?

Does that graph exist in any other form?

As it's molecular weight is 84 mg/mmol we'd need 2.5*84 = 210 mg to raise a source water mash at pH 5.63 to 5.7.

Is the 210 mg per some volume?

Thanks again, I owe you a beer; well probably a case!

 

[ajdelange]

AJ, so sorry you had to input twice. Been burned enough that I've gotten where I copy long posts before submitting for that reason.

I used to do that under the old server. This is the first time the new one has done this to me.

I can't tell you how helpful this was. I have a much better understanding of how it works now.

Delighted to hear that!

I really appreciate you taking the time to explain.

No problem. I do all this in the hope, of course, that I can convey some understanding of how brewing chemistry works to the readership but I also, in trying to come up with clear explanations, often gain new insights. Doing this one twice was one of those cases as the graphical approach came to me after 'sleeping on it'. So no worries about having to do it twice.

Can I infer from above that if my Alkalinity from my water report is 98 ppm as CaCO3 then my alkalinity is 1.96 mEq/L?

Yep. And you might have noticed that this is obtained very quickly by doubling the ppm and dividing by 100 (moving the decimal two places to the left).

Does that graph exist in any other form?

Not sure what you mean here. The graph was cooked up this morning using a visualization program called IGOR by Wave Metrics. It is actually incredibly simple to do one of these once you are comfortable with using mEq units. But I don't have much luck in convincing people to use them. I guess it's like the metric system. It can make your life much easier (which is why scientists use it) yet even in countries that have officially adopted it (Canada, England, Australia) they still cling (to various extents) to the English system. WRT Australia, I'm not sure the 'tinny' ever was an official unit under the English system but AFAIK it is still used as the basic measure of distance.

Is the 210 mg per some volume?

It applies to the test mash of 1 kg malt and 2 L water in exactly the same way as with the acid cases except that here it represents removing 2.5 mEq protons rather that supplying some. Thus it is 2.5 mEq, absorbable by 210 mg of NaHCO3, per kg malt because the test mash contains 1 kg malt. Were you mashing 10 kg grain you would use 10*210 = 2.1 grams NaHCO3 which would absorb 25 mEq.

 

[ajdelange]

I suppose there is an minimum amount required to overcome the tendency to remain stable.

There shouldn't be.

As I watch more videos of home brewers adjusting their pH, most I see just add small amts of acid or base until they get the result they want.

That works too. The math is mainly useful for giving you an idea as to how much acid you are going to need.

 

[dmcmillen]

AJ, I hope you're still monitoring this post. I've been out of pocket for a few days. I am good with calculating the amount of acid required to shift pH. Don't think I'll have any problems there.

Probably going to put my full ignorance on display here; I am having a bit more difficulty with calculating the amount of sodium bicarbonate to shift the pH up. I see exactly how your example worked using the graph, but won't the graph be different for every grain bill? I'm just trying to get my arms around how to generalize the solution in those situations where I might need to raise the pH. Thanks!

 

[ajdelange]

There is absolutely no difference in calculating an upward shift relative to calculating a downward shift. You just see how many mEq of protons must be added or removed. Each mEq added will shift the pH down by about 1/40 pH unit per kg malt. Each mEq removed will shift the pH up by about 1/40th pH unit. But, and I think this is your point here, it isn't always 1/40 the pH unit per kg per mEq. Each curve is indeed different. Each will have different curvature and, more significantly, different slope. The thrust of the argument being advanced here is that you can get an estimate of that slope from a pair of pH measurements which are ideally close enough to each other that the curve is, between them at least, very close to being linear so that interpolation between them and even modest extrapolation outside them is valid.

Don't be thrown by the fact that in the example the acid we used to supply protons was in the form of a solution and the base we used to absorb them a powder. You can very well use the mass approach with lactic acid solution by weighing it out but this requires a balance whereas volume can be measured by simpler means. The trick with liquids is that you must know the density as well as the number of protons per millimole released by the acid or absorbed by the base. For example, a gram of 88% lactic acid solution contains 880 mg of lactic acid which is 880/90.08 = 9.76909 mmol. Now all you need to know is how many protons a mmol of lactic acid releases. This depends on the target pH somewhat. For pH 5.5 this is 0.978 mEq/mmol. Thus 1 gram of solution yields 9.55 mEq protons.
[Edit]Where to get pK numbers? Wikipedia has them for the commonly used acids.[/Edit]

The only part that may seem arcane in this is calculating the number of protons released per mmol. This is actually very simple to do (or rather to program). Here is the code I use

function QQ(pH, pK1, pK2, pK3)
variable pH, pK1, pK2, pK3

variable r1 = 10^(pH - pK1)
variable r2 = 10^(pH - pK2)
variable r3= 10^(pH - pK3)

variable f0 = 1/(1 + r1 + r1*r2 + r1*r2*r3)
variable f1 = r1*f0
variable f2 = r2*f1
variable f3 = r3*f2

return -(f1 + 2*f2 + 3*f3)
end

Not much to it. pH is the target pH. pK1, pK2 and pK3 are the pK's of the acid. If the acid only has 1 proton model the other two non existent protons by giving them huge pKs such as 50. I'll bet you can figure out how to extend this to more protons (though you will seldom encounter acids with more than 3 in brewing except maybe phytic which has 12).

The function actually returns the charge on all the acid's anions which is a negative number. Reversing the sign gives the number of protons that had to have been given up to result in that negative charge.

 

[dmcmillen]

Ok, think I've got it. Keep me honest here. In the example above in wanting to move from 5.63 to 5.7. .07*40 = 2.8 mEq/kg protons to be removed. Since 1 mmol sodium bicarb absorbs 1 mEq protons, then 2.8*84=235.2 mg.

SInce the attached graph is an image, I was originally looking for a version with the data points used to plot the horizontal and 2 vertical axes so that I could generate a graph for each mash. Since I think I understand how to calculate now that will not be necessary.

Just hadn't thought through. As usual when the light goes off, you sometimes wonder how you could have missed.

On a somewhat different topic, I'm curious that John Palmers water calculator doesn't even consider pH. He is only interested in RA. The little experience I have with the other water calculators is that pH is of the greatest importance. I have so far found it almost impossible to hit Palmer's recommendations for RA and get the pH and chemical balance where I want it. Just look at the various water profiles in Martin's program. Many end up with negative RA. Any thoughts?

Thanks again!

 

[ajdelange]

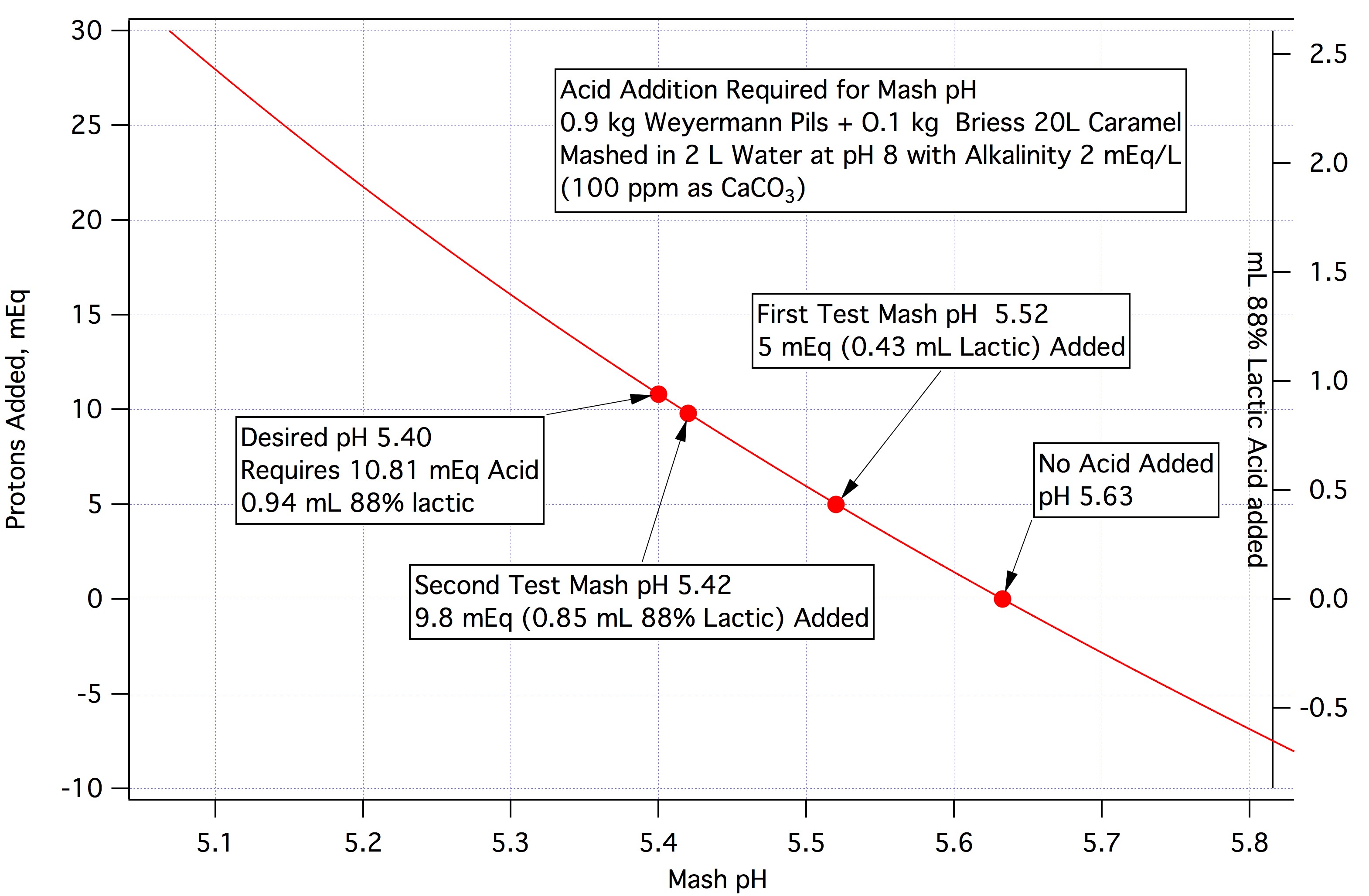
Ok, think I've got it. Keep me honest here. In the example above in wanting to move from 5.63 to 5.7. .07*40 = 2.8 mEq/kg protons to be removed. Since 1 mmol sodium bicarb absorbs 1 mEq protons, then 2.8*84=235.2 mg.

Check.

Just hadn't thought through. As usual when the light goes off, you sometimes wonder how you could have missed.

That's how the mind works. Sometimes, though, it is using the new concept that causes the light to come on. If you actually use the metric system, which people don't seem to want to adopt, eventually you will realize that if the sign says it's 444 km to Ayers Rock it will take you 4.44 hrs to get there if you drive 100 km/hr and it a lot easier to multiply the .44 by 60 to get 28 minutes for the fraction than it is to look at 277 miles which, at 60 mph wiil take you 277 minutes and mentally compute 4:27 from that.

On a somewhat different topic, I'm curious that John Palmers water calculator doesn't even consider pH.

In another thread (https://www.homebrewtalk.com/forum/threads/got-my-water-tested-now-what.647463/) I say

Thus we can say (and often do) that if the water pH be between 6.9 and 9.4 the acid requirement is 90% ± 2% of the alkalinity.

and show why this is the case.
Most of the calculators approach the problem by reasoning that most of alkalinity is bicarbonate in the pH range in which brewers seem to operate. Fifty ppm of alkalinity implies 50/50 = 1 mEq of protons are being absorbed and as 1 mmol bicarbonate will do that in this pH range, the authors assume that 1 mEq of alkalinity is equal to 1 mmol of bicarbonate (61 mg/L). Thus if you have 50 ppm alkalinity they make you convert that to bicarbonate (61 mg/L) and have you enter that into their program. Then that they then convert to an acid requirement which is, as long as mash pH is reasonable and water pH within a certain range, going to be pretty close to 90% of the alkalinity and thus they do not need to consider either mash pH or original water pH in calculating that requirement. Because of the location of the first pK of carbonic acid (6.38) one can get away with this. A robust calculation, such as the one described in MBAA TQ vol. 52, no. 1, 2015, pp. 3-12 Predicting and Controlling Mash pH Using Simple Models for Mash Component Acid/Base Characteristics does, of course, take both mash pH and liquor pH into account. The algorithm defined there computes the protons necessary to be added or removed from each mash component in order to compute a total 'proton deficit' for a given pH. The estimated pH of a mash is the one that causes the total proton deficit to be 0. The total can be written as

Total = deficit_Malt1 + deficit_alkalinity + deficit_water +deficit_Calcium + deficit_Magnesium + deficit_acid + deficit_base...

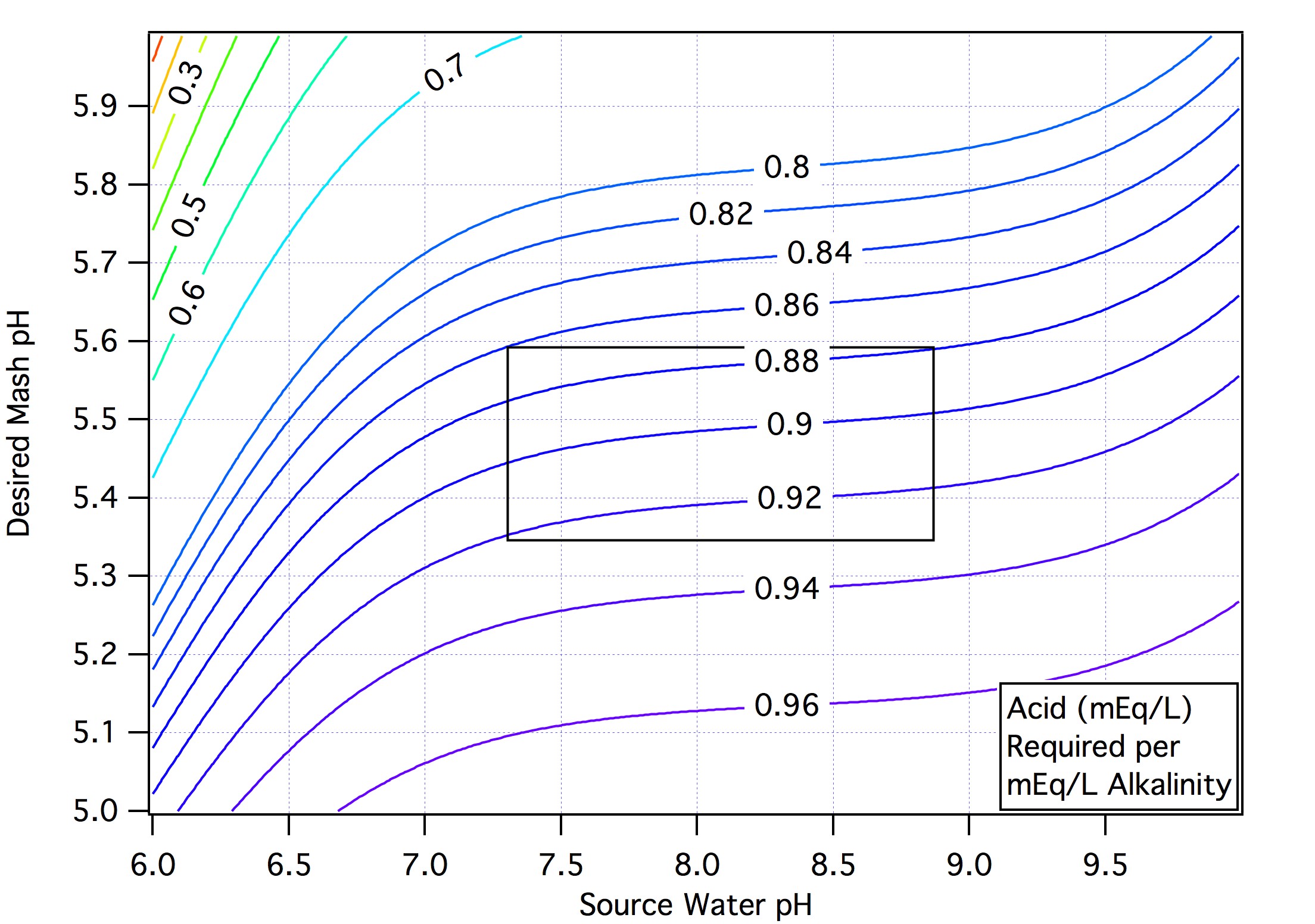
Base malts, bases and alkaline water (contains the base bicarbonate) absorb protons and have positive deficits. Calcium, magesium and acids supply protons and have negative deficits. All the terms in that sum except the calcium and magnesium terms depend on the mash target pH (and they well may too but at this point they are considered to depend only on the concentration of the ions) as does the alkalinity deficit but it depends on the source water pH too but the dependence is weak as following graph shows.

The alkalinity and metal ion sum is thus seen to be, in the boxed region of the graph:

deficit_alkalinity + deficit_Calcium + deficit_Magnesium ≈ 0.9*alkalinity+ deficit_Calcium + deficit_Magnesium ≈ alkalinity + deficit_Calcium + deficit_Magnesium = RA

The formal definition of RA is

RA = alkalinity - [Ca++]/3.5 - [Mg++]/7

Thus the robust calculation includes something close to the RA, i.e. 0.9*RA but not the RA as it is usually defined.

He is only interested in RA.

When John set out to write his book he was convinced that RA was the holy grail of mash pH prediction. I tried hard to convince him that it wasn't and in fact developed the robust algorithm to try to convince him of this. Obviously he accepted it at least partially as some of it appears in the book but he never fully let go of RA.

The little experience I have with the other water calculators is that pH is of the greatest importance.

I don't have much experience with any of them but none of them, that I can think of, ask for source water pH.

Just look at the various water profiles in Martin's program. Many end up with negative RA. Any thoughts?

The problem with Martin's profiles is that he wants certain cations and winds up with the levels of chloride and sulfate he wants with an excess of cations. So what is he to do? I don't really have any bright ideas other than to accept less calcium and magnesium or more sulfate and/or chloride be he has adopted the approach of adding bicarbonate. The problem with that is that bicarbonate's charge depends on pH. Martin decided to use the charge at pH 8.3. As bicarbonate comes to us at pH 8.3 one doesn't have to do any charge shift calculations if he assumes the pH is 8.3. The problem is that if you add bicarbonate to water the pH doesn't always come to 8.3. The short and long of it is that you can't make many of his profiles except at pH 8.3 and I believe his general advice with regard to this is to ignore the bicarbonate column.

 

[dmcmillen]

I am reminded of the old saying about physics advancing one funeral at a time, as the old guard doesn’t seem to be able to let go of their ideas about how the world ought to work in favor of how it actually does work, as shown by the evidence.

That said, it is important to understand that we are all susceptible to this effect.

 

[dmcmillen]

AJ, could you suggest what to use to measure small acid amounts. As I play around with the numbers, scaling down to say a half pound of malt in one case would require .073 ml lactic acid. Pushing that up to a pound isn't much easier. What I currently have is a couple of 1 ml syringes graduated at .1 ml. I have scales that can measure down to .1g so I don't have any problems on the malt side.

Thanks, David

 

[ajdelange]

Probably the simplest way to handle this is by dilution of the stock acid. For example if you were to put 1 ml of acid in a 100 ml volumetric flask and make up to the mark with DI water then 7.3 ml of the dilution would be equivalent to .073 ml of the full strength acid.

 

[dmcmillen]

Of course, another aha moment. Do you think the plastic syringes I got at Walmart are adequate?

 

[ajdelange]

Yes. Calculated acid amounts are going to be ±10% at best so you don't need Class A glassware to measure them out. Besides that it isn't accuracy that is important here. It is repeatability. Suppose your syringe delivers 20% more than its markings indicate. You want to make a 1% solution so you draw up what you think is 1 mL but it is really 1.2 mL so that your dilution which you intended to be 1% is really 1.2%. Now suppose you wind up using, per the syringe, 7.3 mL of that which corresponds, you think, to 0.073 mL stock acid while in reality it is 0.073/1.2 = 0.0608333 mL. Let's say your test mash used a pound of grist and you mash uses 100 (just to make the math easy). You want, thus, 6.08 mL stock acid but would draw 7.3 mL as indicated by the syringe thinking it to be accurate. But just as 7.3 mL of the dilution as indicated by the syringe is in reality 7.3/1.2 mL so 7.3 mL of the stock is 7.3/1.2. The amount of acid you add is not what it appears to be but is in the correct amount. It doesn't really matter how much acid you think you are using. What matters is that it is mass_mash/mass_test_mash time the amount that got the test mash to the right pH.