Open fermentation in a plastic DIY Coolship

[DSorenson]

It is not a coolship, not even a little, and it accomplishes nothing that a coolship accomplishes.

It is a rectangular fermenter that the OP is pseudo open fermenting(which may or may not do anything to produce a different beer).

I would be interested to use differently shapes of fermenters, but it would be difficult to ascertain any difference without a side by side batch in a cylindrical fermenter.

I believe the OP's source did more than enough to show evidence that fermenter geometry has an effect on the finished product.

I commend OP on a job well done and on the brave choice to risk beer in the pursuit of perfection.

 

[orangehero]

I believe the OP's source did more than enough to show evidence that fermenter geometry has an effect on the finished product.

I commend OP on a job well done and on the brave choice to risk beer in the pursuit of perfection.

I would guess when dealing with homebrew size fermentors the geometry is completely irrelevant. Anything you can ferment a 5 (or even 10) gallon batch in is probably more shallow than a "shallow" commercial fermentor.

 

[DSorenson]

I would guess when dealing with homebrew size fermentors the geometry is completely irrelevant. Anything you can ferment a 5 (or even 10) gallon batch in is probably more shallow than a "shallow" commercial fermentor.

We don't really know what is causing this effect, but allow me to make a case:

- What if it is pressure dependent?
If the cause of greater ester production is inversely proportional to pressure in a hydrostatic fermenter, we would very likely notice a difference between commercial and homebrew scale conical fermenters. I say this because the pressure is completely height dependent. The deeper the fermenter, the greater the pressure at the bottom. Since pressure increases linearly (rho*g*h) we know that more beer is exposed to greater pressure in taller tanks. The inverse would be true for homebrew carboys. I hope this has made my case against this idea.

Disclaimer: I am not knowledgeable on large scale brewing concerns, and I welcome anyone with experience to chime in. I have not heard of this being an issue for big brewers, and I am aware that some people ferment under pressure.

-What if the cause is purely in the geometry?
Well we still don't know what's causing the effect; surface area to air, beer contact with flocculated yeast... etc. This asside, we can say is that geometry between commercial and homebrew levels can be proportional. We can compare a commercial shallow fermenting rectangular prism or cube and compare it (using ratios) to one of homebrewing volume.

That is to say that the effects of geometry would be proportional, and therefore similar. We already have an idea about this, since the same beer can be brewed in an 80 hectoliter cylinder as in a 20 liter cylinder.

I think in the end, the OP can speak for it's effectiveness. You might argue placebo, but all anecdotal information is subject to this type of scrutiny.

 

[orangehero]

What effects are you specifically talking about and why are you assuming the effects of geometry are proportional (aside from pressure)?

The depth of liquid (and static pressure) in homebrew sized vessels is less than the shallowest of commercial tanks. On the commercial scale the difference in pressure between a cylindroconical vessel and a shallow fermentor are significant. Not so when you're talking about 8" difference in liquid level between a carboy and a plastic tub.

 

[DSorenson]

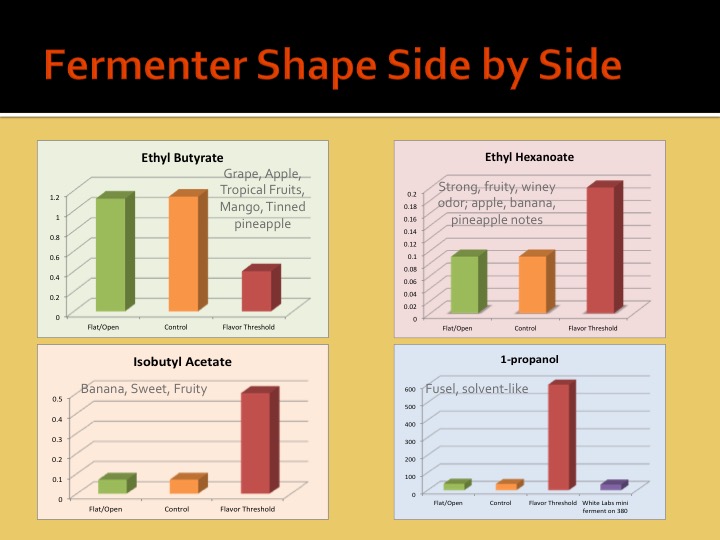
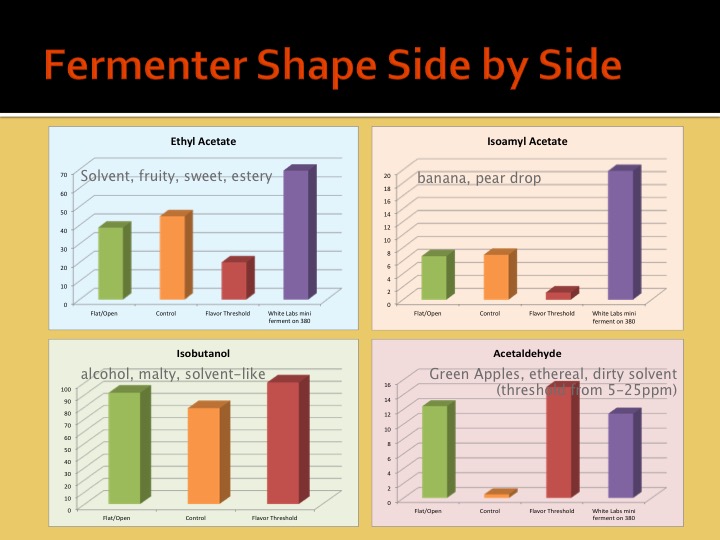
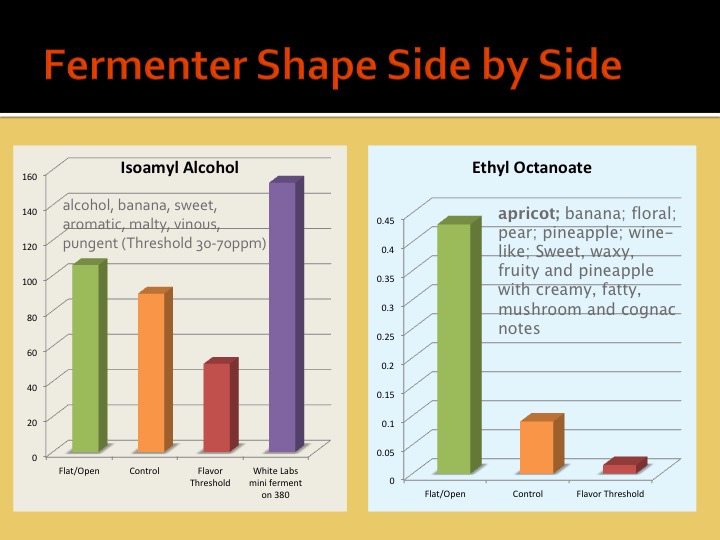
What effects are you specifically talking about and why are you assuming the effects of geometry are proportional (aside from pressure)?

The depth of liquid (and static pressure) in homebrew sized vessels is less than the shallowest of commercial tanks. On the commercial scale the difference in pressure between a cylindroconical vessel and a shallow fermentor are significant. Not so when you're talking about 8" difference in liquid level between a carboy and a plastic tub.

Stick with me, here.

In response to the pressure part:

If we assume that a characteristic of fluid mechanics is responsible for ester increase, then that characteristic would be pressure. Since the pressure goes down in a rectangular prism fermenter, then the ester production goes up when the pressure is less, via our first assumption.

If that was true, then the difference in pressures between commercial brewing and home brewing would be immense and homebrewers would notice increased ester production (relative to style) in every beer we made as opposed to commercial.

This is why I do not believe that increased ester production is a function of pressure.

In response to the geometry part:

We can look at proportionality between any characteristic of a 3D shape and it's volume. It will be a constant value.

Say you have a cubic fermenter that holds some volume "V" of wort and has a base area "A" at the bottom. You can compare, for instance, the area of the base of the fermenter with the volume it caries:

A/V=C

Where "C" is your base area to volume ratio. If you wanted to make a fermenter that holds more volume "V" and maintains the same base area per volume ratio, then you can construct a fermenter with an equal base area per volume:

C*V=A,

Where "A" is the product of the lengths of two adjacent sides of your rectangular base.

The point of this is, in short, that we keep the attributes of what the beer is contacting the same. Two fermenters constructed proportionally in this manor will sit on the same area of flocculated yeast per unit volume of beer. Or it will be in touch with the same area of surface area to air per unit volume.

We must be able to surmise that ester production is proportional to some characteristic of the shape of the fermenter, and not the pressure of the fluid within.

In other words, pressure is the only property at work here for which scale could account for differences. Since pressure is not a likely suspect, then it only leaves the actual shape of the fermenter. Since the shape of a fermenter can be proportional for any unit volume, scale does not matter.

 

[orangehero]

If we assume that a characteristic of fluid mechanics is responsible for ester increase, then that characteristic would be pressure. Since the pressure goes down in a rectangular prism fermenter, then the ester production goes up when the pressure is less, via our first assumption.

It is known that increased pressure suppreses ester production. Because of this reason, commercial brewers are able to ferment at higher temeratures in cylindroconical vessels compared to shallow fermentors and still get the same ester profile.

If that was true, then the difference in pressures between commercial brewing and home brewing would be immense and homebrewers would notice increased ester production (relative to style) in every beer we made as opposed to commercial.

This is exactly what happens. What we do as homebrewers to make a particular beer is not necessarily what is done on the commercial scale. You're assuming that all of these parameters scale linearly in their effects based on batch size, but it's not that simple.

I'm skeptical that differences in surface area at this scale (e.g. between a carboy and a plastic tub) really makes any difference, whether due to contact with flocced yeast or exposure to air (which shouldn't really be happening after CO2 production begins) or whatever else.

 

[DSorenson]

I'm skeptical that differences in surface area at this scale really makes any difference, whether contact with flocced yeast or exposure to air (which shouldn't really be happening after CO2 production begins)

If you can make it out, OP's first post has a picture of the book he got it from. Read the paragraph or two just above the chart, if you can make it out.

edit: for the record, I can understand your skepticism. Also, very cool- didn't know that pressure actually had an effect. Would you happen to have any sources on that?

Also, it looks like the open fermentation is truly the only way to substantially increase esters, from what that chart says.

 

[orangehero]

I have that book, and like I said I'm skeptical that it translates to homebrew scale. I haven't done the calculations, but I doubt that the height of 5 gallons in a slim cornelius keg (that's not pressurized) really creates enough of an increase in pressure than the height of 5 gallons in, let's say presumably a carboy, to result in a noticable difference in ester production as Stan Hieronymus proposes. The paragraph also explains why pressure is the factor at work (by increasing CO2 concentration).

If you get any books on lager brewing they are all about decreasing ester production.

 

[Twinkeelfool]

Ever tried it ?. I have and I'm planning on doing it again, because I liked the results a lot. It's about keeping the ratio of height to width at 1:1 or less. Why does it work? Don't know.

 

[DSorenson]

I have that book, and like I said I'm skeptical that it translates to homebrew scale. I haven't done the calculations, but I doubt that the height of 5 gallons in a slim cornelius keg (that's not pressurized) really creates enough of an increase in pressure than the height of 5 gallons in, let's say presumably a carboy, to result in a noticable difference in ester production as Stan Hieronymus proposes. The paragraph also explains why pressure is the factor at work (by increasing CO2 concentration).

So I did a little math:
The x axis is the radius of the fermenter (cylindrical) in meters and the y axis is the pressure at the bottom of the fermentor in Pascals. (metric was just easier). Here, I am using 5 gallons of water just for reference (18.9 L).

It does seem to me that these pressures are not that significant when compared to pro brewing setups. A 6 gallon better bottle filled with 5 gallons of water has a radius of about .145 meters and has an ultimate pressure of 2824 Pascals. (about 3% of the atmospheric pressure at sea level)

This is nothing compared to a 1:1 height:diameter (cylindrical) ratio for an 8000 liter setup (80 hectolitres), which is 212439 Pa. That is roughly two times the atmospheric pressure at sea level.

Okay, so now we know what we are dealing with here.

I will say this: If it's true that larger breweries adjust for pressure differences when brewing in a "standard" vessel, then the results of homebrew ideally mimic those of a larger scale. With this in mind, perhaps scaling down the pressure for either results in increased ester production.

In other words, perhaps the effect is the same even if the pressure differences are huge?

This would be easier to figure out is someone would just give me some formulas relating pressure and brewing...

 

[mcbethenstein]

Wow,
There has been quite a bit of discussion on this while I was gone! Suffice it to say, perhaps the depth of the fermenter on a homebrew scale has less to do with the increased ester levels than the psuedo-open aspect of it. But it does make a difference… and a tastable one at that. Even the non-super tasters at our learn to brew day could distinguish the highly ester-y characteristics of this beer. I am still inclined to believe that ratio of surface area to depth is a deciding factor (Although NOT the sole factor). With that level of surface area there is a freer exchange of Oxygen and CO2. Most brewing science out there suggests that increasing Oxygen will actually decrease ester production, which is opposite of what we are seeing here. However there is also info out there that suggests that increasing CO2 concentrations also "scrub your beer" clean. Off flavors and esters are picked up by the CO2 and then driven off after the CO2 is pushed out of the beer and through our blow off tube or airlock. With so much open space, CO2 off gases easily and with decreased concentration in the wort and decreased contact time may allow for more esters to remain in the finished beer. Here is a powerpoint from David Bryant at the Brewing Science Institute that summarizes the findings of many major studies by the german Hefe brewers. It is far less technical and more understandable to me than a number of other references I've come across lately, along with real world observations by the brewers themselves.

http://www.mbaa.com/districts/MidSo...2010-03-13Wheat_Beer_Yeast__Fermentation2.pdf

 

[g-star]

Thanks for sharing that presentation, very informative. I find German wheat beers to be very difficult to nail...lots of great info there.

 

[ABVIBUSRM]

King'd!!!!

 

[mcbethenstein]

So, I thought this tread could use a little update. I decided (was highly annoyed by my club leader) to submit a proposal to speak on at NHC 2015. I was accepted and spoke on the two experiments I chronicled here on HBT and on another.... This Fermenter shape.

I finally put together a side by side full scale 5 gallon brew to compare the fermenter shape...ON A HOMEBREW LEVEL. You are all familiar with the build, so I will get right to the process. This past February I did a 10 gallon brew day with a friend. We did 2-5 gal batches of my Hefeweizen and then blended them into one batch to control for any mashing differences. I poured 5 gal into the bucket fermenter, and left 5 gal in the flat/open fermenter. I oxygenated each for 30 seconds and then split my yeast (from one starter) into two equal pitches.

Fermentation took off pretty quickly. Both had huge krausens and the traditional bucket had a blowout. After the fermentation completed both were transferred to keg to condition with DME and 2 samples were collected to send for analysis with White Labs analytical lab.

 

[mcbethenstein]

The analysis came back a few days later and I spent many hours tracking down ester names, descriptions and threshold levels. The following slides show the differences in the two batches. The first slide shows the esters that had relatively stable counts (in ppm) as the control. The Green bar on each is the flat/open (coolship style) fermenter. The orange color is the control batch in the plastic bucket. The red bar is the flavor threshold for human detection in beer. And if there is a purple bar, that is the mini ferment data from white labs on WLP380 (available on their website)

The second slide are the esters that there was a difference. Even if slight. I have to say I was expecting a difference in Isoamyl Acetate (the dominant banana note in German Wheats) but it was the same.... BUT The third slide shows that the Ethyl Octanoate was almost 5 TIMES higher than the control, and given that the dominant flavor that WLP380 puts out is apricot (from Ethyl Octanoate) this makes sense. The other striking difference was with Isoamyl Alcohol where the flat/open Hefe was at 106 ppm, the control was 89, and the taste threshold at about 50ppm.

Taste tests concluded that there was a difference. 5 Tasters tried both versions side by side and could tell the difference between the two, however 4 of 5 preferred the traditional bucket version, because it was more "Hefe-like." 1 preferred the more fruity nature of the flat/open.

I think I would like to try this experiment again with WLP300 to try the more traditional strain that most Hefe drinkers are expecting. The Flat/Open fermenter got much better attenuation with a final gravity of 1.006 and dropped clearer, while the bucket attenuated to 1.011 with a slight bit more yeast left in suspension.

 

[tagz]

Wow. Nice work! Very interesting stuff. I know hefeweizens are your thing, but I would love to see a saison version of this experiment. So, the levels were just below the taste threshold, but did you pick up any solvent or acetal in your tasting? Also, which did you prefer?

 

[ArcLight]

I noticed that the open fermentor had much more (by a factor of 10) Acetaldehyde, but it was still below (though near) the detectable threshold. I wonder if conditions were changed a little (slightly less healthy yeast) if the taste threshold would be reached, and the beer not taste as expected?


As for the 5 tasters preferring the control sample - it may be because:
1 - that's the flavor they are used to
2 - the flat fermentor isn't quite to style

Had brewers always used flat fermentors , maybe the tasters would prefer the flat fermented beer, saying the bucket was missing Apricot flavor and didn't taste to style.

I personally am less interested in brewing to style, and more interested in making beer I like.
The style was influenced by technology (or lack thereof). For me, I wouldn't want to be limited by it.

 

[Gavin C]

Great Read. Thank's OP for all the hard work that has gone into this. I trust your speech at the NHC went well. Very nicely documented. Really loving all the pictures illustrating things.

 

[mcbethenstein]

To answer a few questions...
On the acetylaldehyde, I did not detect it, nor was it mentioned by any of the tasters. I did pull an early few bottles of the flat/open Hefe and send them to midwinter competition. It didn't score particularly high, to the judges the banana was too muted, they could not pull out the apricot notes, but none mentioned acetaldehyde, so it was definitely below the threshold of a few trained judges.

ArcLight - to answer all your questions, I think you are right about the tasters preference. It was different, but not so drastically that they couldn't tell it was a Hefe. The yeast health obviously is a factor in this fermenter shape given that the yeast flocculated out faster with the flat/open. I have read/heard that open fermentation yeast will get full and lazy and floc out, but it would result in a stuck fermentation, so as part of my process for this fermenter, the yeast are roused during skimming. To address how I split the starter (question from your PM)... I too was concerned about stratification so I poured out in 3 rounds. Putting the starter back on the stirplate between pours. I hope I got a good split (as close to 50/50) as is humanly possible without starting with lab counted samples. I considered pitching 1 vial into each, with the same manufacture date, but I only had access to 1 vial at the time I conducted the experiment.

My preference was for the flat/open fermented one when I tasted the beers before sending them to analysis, then I preferred the bucket at the time I did the taste testing, afterwards I preferred the flat/open... It really keeps changing. As the beers have aged the differences are smoothing out. The strength of the apricot has subsided (as we know esters are prone to do with time) and the remaining yeast in the control has dropped and the yeast bite that may have been the "Hefe" character that my tasters preferred is deminished as well.... But it may be time for a last taste test before I kick the kegs (each has about a gallon left)

 

[mcbethenstein]

It's application time.... Yesterday I was a bad scientist. I brewed my Hefe again, but made 4 changes! Agh too many! Just kidding. With all my prep for NHC I ran across old notes and some new realizations. I swapped out my bohemian wheat for the rahr red wheat. (I want to see if the rye like creamy flavor translates into my Hefe) Lowered my ferulic acid rest to 104°F (per my reference journal). Pitched WLP300 instead of WLP380 (due to Availability and curiosity), AND here's the big change... Monitored my pH into & out of the kettle and adjusted down. (Referenced in brewing with Wheat... Schneider does this. They feel if wort pH is too high they lose character) I found average into fermenter pH is supposed to be 5.1-5.3. Mine was 5.7 so I adjusted down to 5.07 with lactic acid... A little lower than my 5.1 target, but close. This COULD be the final adjustment that makes my flavors pop. They are there in great balance, but have been muted. My spring water is very high carbonate, and then the RO I sparge with (which I don't adjust) had my into kettle pH at 5.81.... A bit too high. I do adjust pH in the mash, to 5.3.

Fermentation took off this morning. After pitching at 66°F temps rose to 69°F by 11 am and 72°F by tonight. It smells amazing so far. Much clove-ier than my last few batches. And a really healthy fermentation. (Pitch of 8 mil cells/mL) it's starting to produce banana and hints of vanilla. Little to no sulphur. In my research, I found that pitch & oxygen influences the balance of the esters and phenols. And temperature controls the intensity (skewing the esters as you go very high). I've followed this principle since I had a few really great hefes from fellow homebrewers, one fermented at 63° F. So I've tried fermenting at 62-65°, but all my score sheets suggest a higher temp, as the balance is there, but restrained for a Hefe... Hence letting the free rise. View attachment ImageUploadedByHome Brew1434948010.023240.jpg

 

[ArcLight]

>.. Mine was 5.7 so I adjusted down to 5.07 with lactic acid...


1. How long is the Ferulic Acid rest? Does it also lower the pH and by how much?

2. Your mash temperature should theoretically activate Phytase to further acidify your mash.
But I think it takes several hours, so its probably easier adding the lactic acid (or Phosphoric acid - since lactic acid may add a flavor above a certain threshold).

 

[mcbethenstein]

1. Ferulic acid rest is 30 minutes. The minimum needed to see a large jump in Free Ferulic Acid to bump up 4VG. No it does not really acidify the mash. My ferulic acid rest sat at 5.76. Then after infusing my highly carbonate spring water to bring up to sacc rest the mash measured in at 5.89. A bit too high for good extraction. So I adjust downward with Lactic Acid. 6.5 ml brought it to 5.31. I did not check the sparge water, but it is pure RO (guess pH of around 7.0)... And I batch sparge. Into the kettle I was at 5.81. After boiling I was down to 5.7. Hence the adjustment. I wanted to target 5.1-5.2 for my into fermenter pH, and over compensated slightly. I am finding conflicting information about taste threshold of Lactic Acid, but have found at least 3 references that german brewers are adjusting pH into the kettle with wort soured with lactic acid producing bacteria and no residual lactic taste. Schneider Weiss adds wort soured to pH of 3.0 (but the book did not reference how much of the wort that was.) Weyermann claims you can use up to 10% acid malt without tasting it... so that would be equivalent to 1.25 ml/lb grain. At 10.25 lb grain bill, I could add up to 12.8 ml lactic acid without taste implications. With my after boil adjustments, I am right at that threshold....

http://discussions.probrewer.com/showthread.php?6608-Lactic-acid-addition-during-boil

Brukaiser's lactate theshold experiment found that the perceivable threshold is easily over 8-10%, in fact close to an average of 13%, so 8% sauermaltz is not unreasonable. http://braukaiser.com/wiki/index.php?title=Lactate_Taste_Threshold_experiment

 

[orangehero]

How much lactic acid did you use to get it from 5.7 to 5.07? You can always try using phosphoric acid if you are concerned with the flavor of lactic acid.

Your pre-boil pH of 5.81 and post-boil pH of 5.7 both seem a bit high to me. It should be more along the lines of 5.4 - 5.5 into the kettle and drop down 0.1 to 0.3 after boiling. I would maybe look closer at your mash acidification.

Are you also comparing this trial with fermentation in a carboy?

 

[ArcLight]

How much lactic acid did you use to get it from 5.7 to 5.07? You can always try using phosphoric acid if you are concerned with the flavor of lactic acid.

Your pre-boil pH of 5.81 and post-boil pH of 5.7 both seem a bit high to me. It should be more along the lines of 5.4 - 5.5 into the kettle and drop down 0.1 to 0.3 after boiling. I would maybe look closer at your mash acidification.

Are you also comparing this trial with fermentation in a carboy?

She mentioned "highly carbonate spring water".
If the water has a high RA it's going to interfere with the pH drop of the mash.
Hence the need for acidification.

 

[mcbethenstein]

She mentioned "highly carbonate spring water".

If the water has a high RA it's going to interfere with the pH drop of the mash.

Hence the need for acidification.

Correct. Sadly, my yeast accentuated the pH drop during the fermentation as lower pH worts are supposedly prone to doing, so I'm sitting on a Hefe with a finished pH of 3.75. A drop of 1.32, well over the 1 point drop that I read to expect. I'm going to have to change my brewing water. There is WAY to much residual alkalinity, and the buffering action has me using too much Lactic Acid. I tasted my Hefe during the fermentation and it's good. Higher clove levels than I've achieved before, but as a super taster, I can pick out the lactate. I won't be submitting this to competition and I will be figuring out how to adjust the water to get my into fermenter pH closer to 5.3(ish) without excessive Lactic Acid. I need to zero in on that balance between enough acidity to make a flavorful Hefe, but not so much that it is overboard. I really wish I had readings on my last few brews to see where they were into & out of the fermenter.

Sorry for the tangent. This batch is not a side by side experiment. Just documenting putting the flat/open fermenter into practice.

 

[drchris83]

Being in the process of perfecting my Hefe as well (albeit at an earlier stage) I can only commend your effort. Also, if you can get your habds at a bottle of Schneider Weisse, you have their house yeast strain in your hands as well. It is general practice among German home brewers to reculture from unpasteurized bottles of commercially available Weizen. Seeing as you use a very scientific approach, I imagine this to be within your grasp. If you speak any German, I recommend hobbybrauer.de and its vast archives - there is similar research being done there. Also, there have been blind tastings of split batches fermented with different yeast. WLP 300 was never among the favorites, whereas beers fermented with recultured yeast from commercial samples. All of this nonwithstanding, I think it's time for my rectangular lautering vessel to get a second job...

 

[ArcLight]

Correct. Sadly, my yeast accentuated the pH drop during the fermentation as lower pH worts are supposedly prone to doing, so I'm sitting on a Hefe with a finished pH of 3.75. A drop of 1.32, well over the 1 point drop that I read to expect. I'm going to have to change my brewing water. There is WAY to much residual alkalinity, and the buffering action has me using too much Lactic Acid. I tasted my Hefe during the fermentation and it's good. Higher clove levels than I've achieved before, but as a super taster, I can pick out the lactate.

1. (genius idea I admit) Use less Lactic acid.

2. (another genius idea that I'm sure no one ever thought of) Blend your water with a couple of gallons of soft RO water

2. I've never done it, but I'm dying to know how well an long acid rest works.
Let me try some subliminal coaxing -
Do a 4 hour Phytase rest at 95F for 4 hours and post the results
I guarantee it will make a great Hefe. I'll prove it.
Send me a bottle of the beer, and being a "super taster" (I like to taste beer!) myself I'll give you a fair and balanced evaluation

(I wish I had a better palate, I can't taste Diacetyl when others do)

 

[mcbethenstein]

Ok, Here is the latest update. On 6/30/15 I ran a double brew day (night), and brewed my Hefe and a BIAB Wit. I backed WAY off the Lactic acid and used store bought RO water for the majority of my water. (I couldn't pull enough from my filter in time) I mashed in with the Spring water and hit 5.74 pH... just a smidgen under my target, but really close for the ferulic acid rest at 105. Rested about 30 minutes. (my detailed notes are at home, and I am not) Infused to hit 154. Decoction to hit 158-160. I only used RO water after the ferulic acid rest. I did pH adjust for the mash and out of the boil, but it was less Lactic Acid than last time for a total of 6.5mL of Lactic Acid. Into fermenter pH was adjusted down to 5.5. Finishing pH was 3.9. A drop of nearly 1.6, again way higher than expected. I did use the flat/open fermenter and would be curious to do another side by side and see if the pH drop is as high with this yeast in the bucket. (I switched back to WLP380 for this batch). I fermented warm. Pitched at around 68 and let it free rise to 72 at peak fermentation. Fermentation was complete at 3 days. I was in a rush to bottle for competition and bottled at 4.5 days after pitch. I was worried that this was too quick, but my worries were unfounded, as it was at terminal gravity and was relatively clear (yeast had flocked). I sent it to two competitions and am glad to say that I finally broke my dry streak! While I was tinkering with it I had not placed with this Hefe since 2012. I won Gold with this beer yesterday at the 2015 Germanfest Stein Challenge, and won a blue ribbon and was Grand Champion Beer at the Waukesha County Fair (admittedly a VERY small 1st year competition). This beer is the best Hefe that I have produced, and is closest yet to what I have been trying to achieve. At this point the only criticism from the judges was a thiner body than world class examples... but not so thin as to lose many points. I will look into whether just a higher mash temp is needed or if my aggressive fermentation thinned the body as was suggested. I bottled to about 3.5 volumes, and I think that REALLY helps in competition with a hefe. I shall see if the kegged remainder has the same expression as the bottled few... It was kegged with DME and naturally conditioned as ALL Hefes should be.

An update on the previous batch: The over acidified hefe was not thrown. I infused a oak spiral with tequila and then infused that tequila with peaches. Tossed it all in a keg and called it El Hefe Reposado, and served it a local festival. Tequila Barrel Aged Peach Hefe =Huge Hit. And not a loss of beer and ingredients for me.... Those hooligans at Firkin Fest will drink ANYTHING.

 

[bembel]

Greetings from Boston..

I pitched my 15th hefe of the year on Friday ( all slight variations of the basic Bee Cave recipe) trying to hit the clove I so adore in Weihenstephaner and Franziskaner)

I have done decoctions, multi step mashes, low temp, mid temp, multi-temp fermentations using every Torulaspora Delbrueckii variation and still can't nail down the flavors that the commercial hefe gods achieve. So last Friday, I decided to try it open, in a 8 gallon bucket inside my keezer for the first 2-3 days, then I googled Open Fermentation homebrew and found these threads, so I am glad to know I am not the only insane one. Peace at last.

So thinking now that shape is a potential variable, Im looking for a suitable 'coolship' that will fit well inside my keezer, which is only 15.5 inches wide, x 24 long before the hump, so many of the low tote -like tanks don't fit. The fish tank idea is a good one, but hard to lift in, out.

Current batch is 20 hours in and I am about to go home and skim, this one is set at 63 and was pitched at 60 with 3056 in a 1 liter starter.

Happy to collaborate with anyone on anything, just glad that there are others willing to chase this dragon with me.

 

[adamranders]

Hello from next door in Brookfield, this is an awesome thread. Congrats on the wins, and keep it coming, thinking about trying a coolship setup one of these days myself, might have to have a go at this.