I'd think in the first case we would actually want both our customers to notice the difference and to show a preference for one or the other. If planning to make such a change I'd want to be convinced customers will be able to tell the difference, and that they show a preference for the more expensive process.
I agree 100% but am, at this point, in a bit of a quandary over this. In my earliest posts in this thread I said that a triangle test consisted of two parts in the first of which panelists were asked to pick the odd beer and then those who correctly picked the odd beer were asked whether they preferred it to the others. I made that assertion because when I was first introduced to triangle testing via the ASBC MOAs that's how the test was described. There were two tables in the MOA. One for significance levels on the odd beer selection and one for the paired test. That second table is not in the current version of the MOA. Beyond this the ASTM triangle procedure specifically states that one should NOT pair a preference question with the odd beer question as having to select the odd beer biases ones choice of the preferred beer. I cannot for the life of me see how this would be the case. I'm still thinking about this. I know I should go delve back into the ASBC archives (if I remembered to pay my dues this year) but am currently working on being sure that I understand the first part of the test (odd beer selection) thoroughly. Insights keep coming.
In the second case since we are hoping customers don't notice the change so there would be an expectation going into the study that the preference data will not be meaningful.
In this case if the sales loss from the cheaper process isn't greater than the cost savings you are ahead of the game and don't care that some small percentage of the customer base doesn't like the beer any more. But suppose you decide to try adding more rice and water and less barley and find the customer base prefers the new beer! Nirvana! Bud Light. So you may care about preference in this case too.
I do too. I've been doing this stuff since the late 60's but still have to check on which is Type I and which is Type II error. And every time I have to do that I picture Kevin Klein in "A Fish Called Wanda" asking "What was the middle thing?" I do believe, however, that AZ_IPA has forever solved that problem for me. It's the look on that guy's face.To be honest I still get lost in the math and have taken statistics and am not repelled by the science.
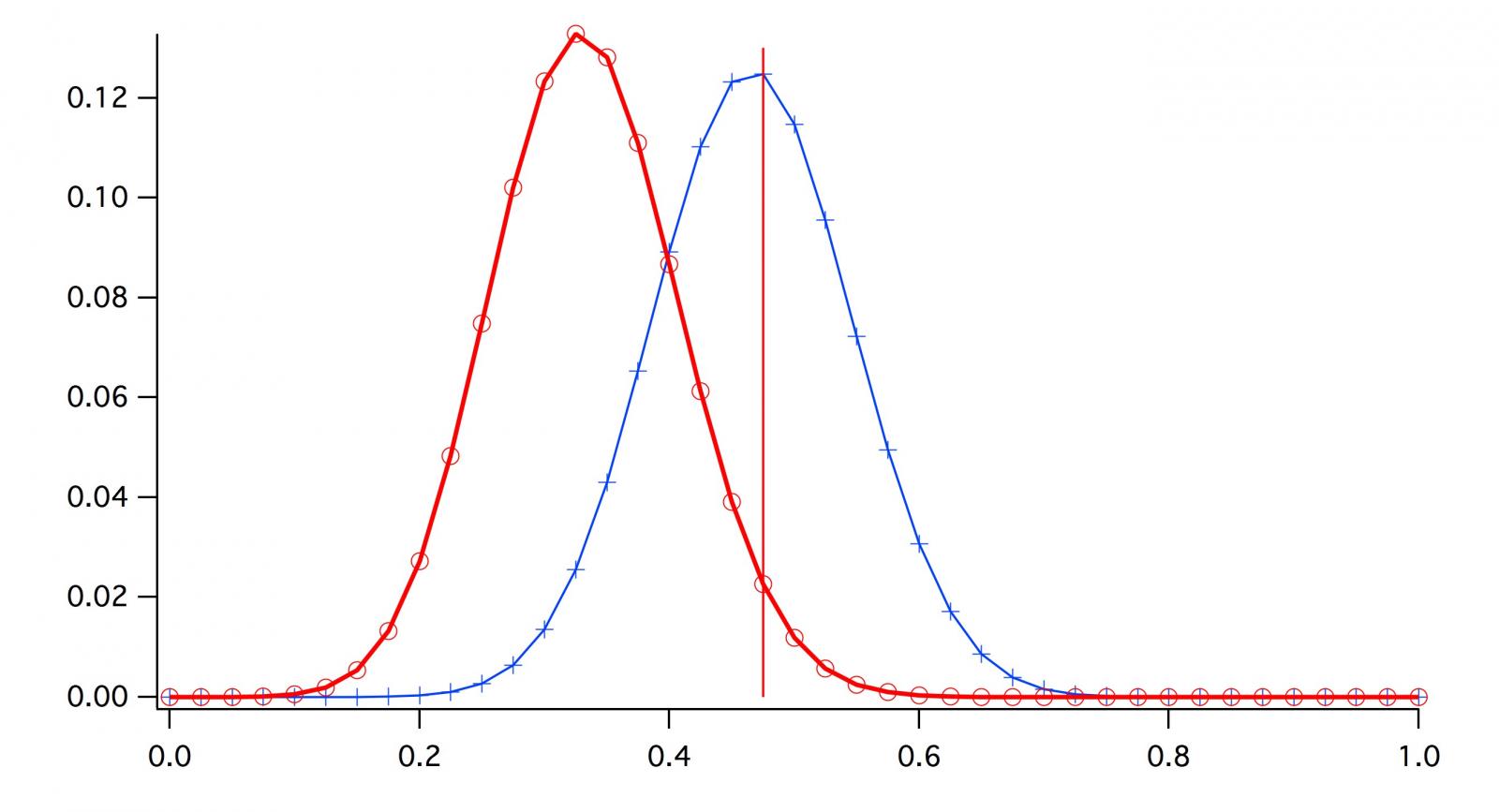
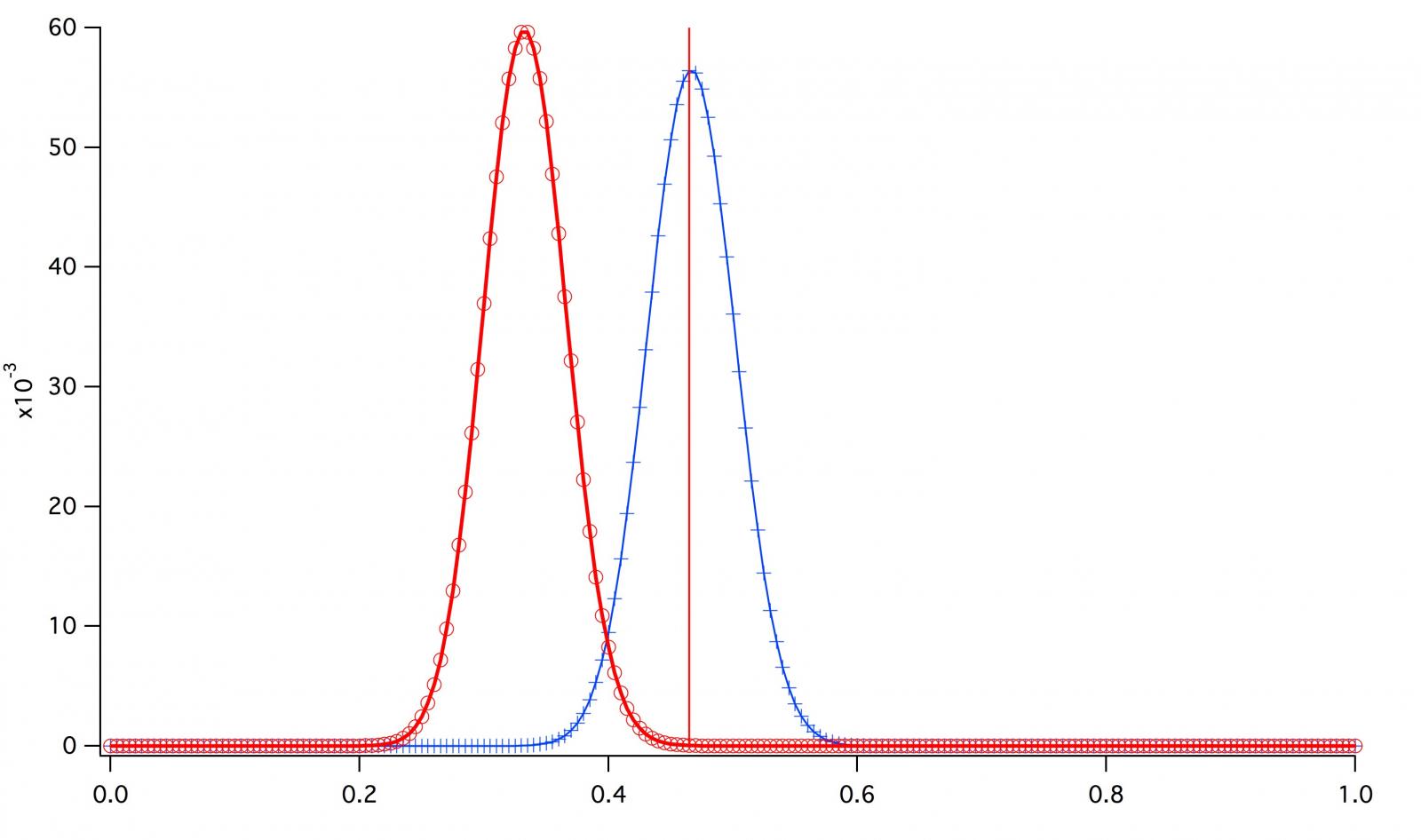
I've often stepped back after an analysis and said to myself "Why did I go to all that trouble? It's kind of obvious from the raw data!" If we have enough data it usually isn't necessary to do more than look at the mean and standard deviation and, based on experience, draw a conclusion. It's often obvious whether that conclusion is 'significant'. We use statistics when we don't have enough data. Statistics attach a number to our uncertainty. We can declare that p < 5% for a test to be meaningful. How about p < 7.2%. Are you really that much more assured at 5% than 7.2%. In either case you are uncertain.But I'd of reached the same conclusions as your two hypothetical brewers in this example simply by looking at 14/40 result.
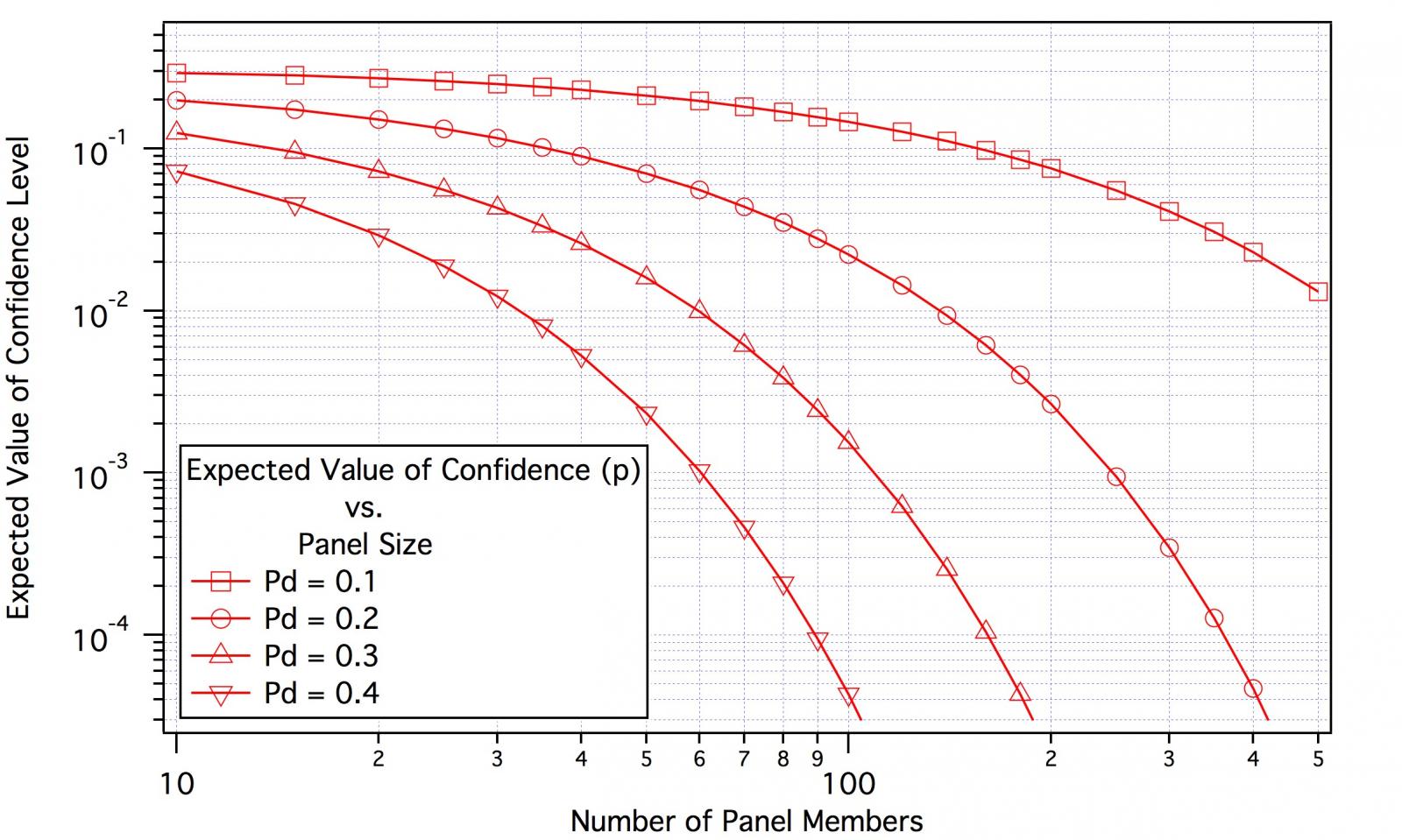
Looking at several of the Brulosophy tests as I did a couple of posts back it is clear that the main criticism that could be leveled against them is that they use panels that are too small to allow them to draw firm conclusions.


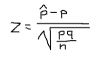



































![Craft A Brew - Safale S-04 Dry Yeast - Fermentis - English Ale Dry Yeast - For English and American Ales and Hard Apple Ciders - Ingredients for Home Brewing - Beer Making Supplies - [1 Pack]](https://m.media-amazon.com/images/I/41fVGNh6JfL._SL500_.jpg)