What do you mean by that? My understanding was that the residual alkalinity accounts for apatite reactions in the mash. And as such, we use it to determine the mash pH. What does it have to do with the boil?
Re-read Kolbach's paper (at
http://wetnewf.org/pdfs/Brewing_articles/KolbachPaper.pdf if you don't have it handy). A relevant quotation is
"From the previously mentioned laboratory experiments it can be concluded that a water of 10° residual alkalinity raises the pH of a 12°P wort at knockout something like 0.3 when one compares the pH with the pH of a 12°P knockout wort prepared with distilled water. A water with a residual alkalinity of –10° will, by contrast, lower the pH of knockout wort around 0.3."
Everyone grabbed the 10° and 0.3 pH numbers and used them for mash pH prediction until someone noticed (and I, who translated this paper hadn't) that they referred to knockout wort).
10Ca++ + 6H2PO4- + 2H2O = Ca10(PO4)6(OH)2 + 14H+
If you look at that it implies that you get 14/20 = 0.7 mEq of alkalinity-cancelling protons for each mEq of calcium precipitated. Kolbach in the paper says it is more like 1/3.5 = 0.28. Thus, clearly, not all the calcium in the mash participates in the reaction and we know this to be true as pH continues to drop in the kettle because of additional apatite precipitation.
Kolbach's 0.3 pH per 10° implies some value of mash buffering which would depend on the mash thickness and the types of malts he studied. As part of pH estimation we are calculating malt buffering so rather than relate mash pH shift to the 0.3 pH per 10° change in RA I have interpreted the observation that 3.5 mEq of calcium or 7 mEq of magnesium cancels 1 mEq of alkalinity to mean that 3.5 mEq of calcium or 7 mEq of magnesium releases 1 mEq of protons. The effective pH shift attributable to those protons is their number divided by the buffering of the total mash. Since everything else in Kolbach's paper refers to knockout wort I assume that 3.5 and 7 apply to knockout wort as well and that the number of protons released by 3.5 mEq of calcium or 7 mEq to the mash must be somewhat less than 1 mEq. In my spreadsheet I use 3.5 and 7. As this results in small pH shifts in most cases I don't worry too much about the error this may cause.
Good idea. However, this won't affect the calculation in any way, since you plug in the amount of acid and the endpoint pH that you got, regardless of the number of additions.
That's right and since it doesn't, we might as well make it as simple for the brewer as possible.
How linear is the pH(temperature) function? In other words, how accurately does a constant glide coefficient reflect it?
Reasonably well, I'd say.
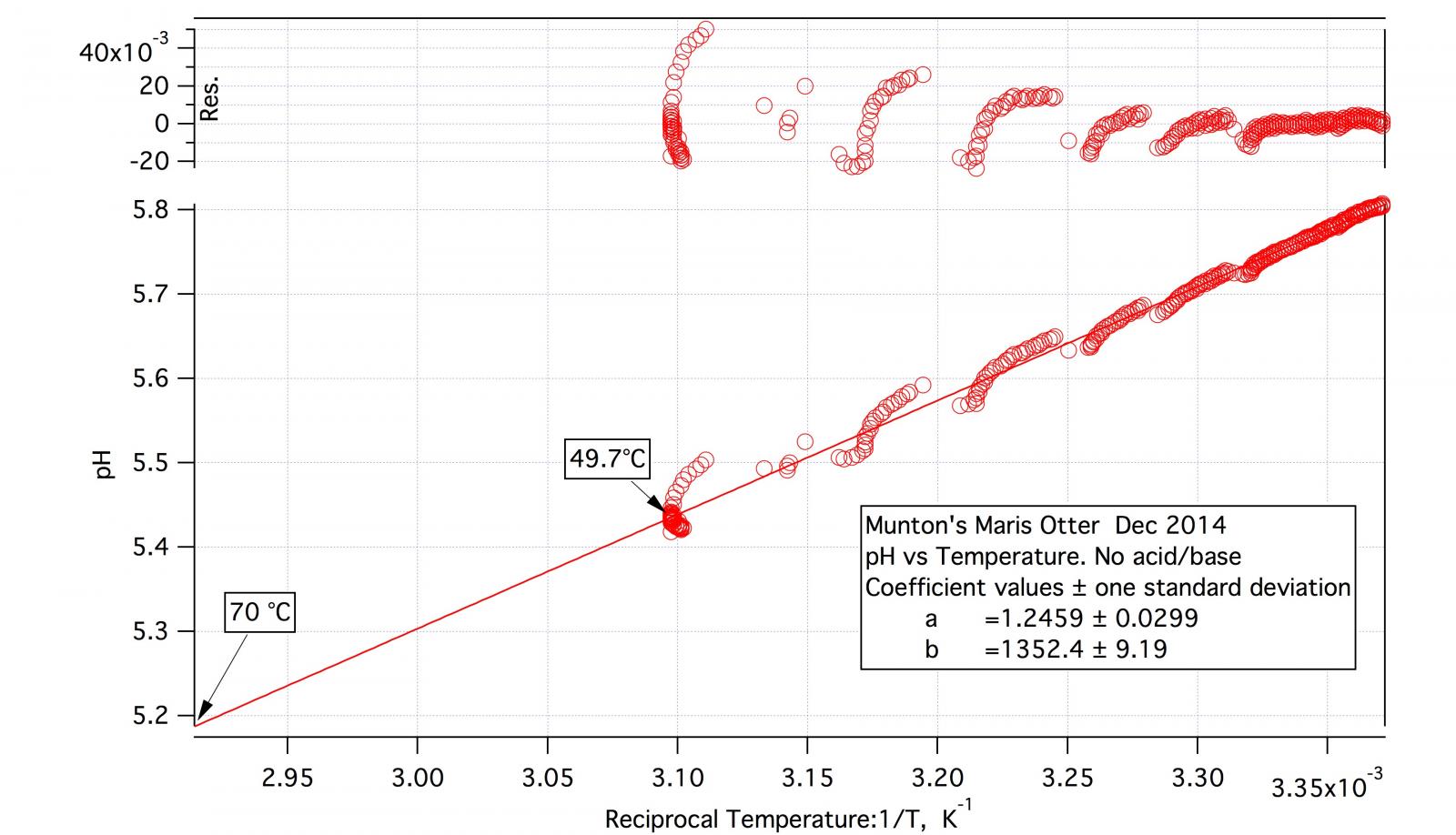
Do you calculate this glide by measuring DI pH at 45°C than cooling down to 20°C, measuring again and dividing the shift by (45-20)?
As the detailed procedure for the malt titration indicates the test mashes, including the DI one, are made at about 50 °C and pH is recorded continuously over half an hour or so. At the conclusion of DI pH recording the mash is then allowed to cool while recording continues. I may, after appreciable cooling, increase temperature again. The result is a block of data of pH vs. time and temperature vs. time. I plot pH vs temperature and then do a straight line fit. It certainly isn't a perfect fit but it's not bad.
What about the the rest of the titration curve and the other coefficients?
Do they change with temperature as well?
They are bound to somewhat but the assumption is that they do not. I haven't verified this, IOW I haven't checked to see if the glide with 20 mEq/kg acid added is the same as the glide with 0 mEq/kg (distilled water mash). If it were terribly different I wouldn't be able to predict room temperature pH using this method and I can do so pretty well in the cases I've tested.
In my mind this is a far more important issue than assuming the correction H3PO4 dissociation of 1.0089 mEq/mmol at pH=5.2 and 1.024 mEq/mmol at pH=5.6.
It is an important issue and we certainly need to understand it better and verify that is is a manageable issue. The supposition is, at this point, that it will introduce a small error. Failure to account for time introduces a small error. Assuming that molar solutions of sulfuric, phosphoric and lactic are, respectively 2, 1 and 1 normal introduces small errors, assuming that the bag of Munton's M.O. I buy and measure today is the same as the one I buy and brew with 5 months from now introduces small errors (or we hope they are small). All these small errors eventually add up and so my philosophy has always been to go after any that I can easily deal with. Certainly computing the normalities of the acids is easy enough to do and can be done without compromising the requirement for a clean, simple user interface. So I do it. Measuring every bag of malt that comes into the brewery to the extent that a1, a2 and a3 can be determined accurately is out of the question so I live with that one.
First off, what is our basis for measuring mash pH and malt parameters at 20°C? Does it really reflect the chemistry in the mash?
Yes, it does reflect the chemistry of the mash to the extent that it is a useable metric for controlling the brewing process. I often use the analogy of altimeter setting in an airplane. Above 18,000 ft (FL180) the altimeter setting at the nearest airport (which may be hundreds of km away in, for example, transoceanic flight) does not reflect the actual pressure conditions at the aircraft's location so all aircraft set their altimeters to 1013 mb. When the altimeter says, under those conditions, 24,000 ft the aircraft is not (very probably) at 24,000 ft but another aircraft whose altimeter is also set to 1013 mb and which also reads 24,000 is at the same altitude, whatever that may be, there is potential for a collision. Thus while it is clear that the altimeter does not read the correct altitude pretending that it does allows safe operation of the airspace.
In brewing a mash pH of 5.4 doesn't tell you what the actual mash pH is at beta glucan rest temperature, protein rest temperature or any saccharification rest temperature but you know by experience that if you set your room temperature mash pH to 5.4 you get better beer than if you set it to 5.5 and so you aim for 5.4.
We use lab temperature largely because when brewers started measuring pH they didn't have accurate meters that slipped into shirt pockets. They had a bulky set of gear in the laboratory. By the time a sample was transported to the laboratory it would have cooled. Furthermore, the meter probably used a calomel reference cell that would melt at mash temperature and temperature stress on the pH half cell induced by measuring hot mash/wort shortened its life. Beyond that, there would be a problem with talking about pH in the literature. It's much easier if all pH measurements are referenced to a standard temperature.
If pH during the mash determines the flavor, it happens at the mash temperature. How does our measurement at 20°C correlate with the actual pH that affects the chemistry?
The point is that it seems to correlate with the quality of the produce irrespective of how it correlates with the details of the biochemistry. The pKs of acids are temperature dependent so it is natural that the pH of a buffer system is going to shift. That's why the buffers we use to calibrate our pH meters have pH vs temperature data on their labels. They are just as useful at 50 °C as they are at 20 °C as long as you have that data.
I know there is a standard procedure. I'm just thinking there may be a way to simplify it for the homebrewer like dough in at 20°C and then measure the pH. There is a limit to what precision a homebrewer can achieve.
If you are referring to procedures for measuring malt parameters there is no standard procedure. I have proposed one and published it. If the industry thinks what I have suggested is a good idea then ASBC and/or EBC will study what I have proposed, quite possibly suggest improvements, publish proposed standard methodologies for implementing it, do collaborative studies and if things work out, adopt the method. We are a long way from that and I sort of doubt that any of this will come to pass.
As it stands now, I don't think I will be rewriting the entire thing to create a second page with the more explicitly stated formulas. Also, I don't like constantly switching between different pages in Excel, maybe that's why my entire water spreadsheet occupies only 1 page. Tracing references to another page is not my idea of convenience.
I'm not trying to load you up with work or tell you how to organize your spreadsheet but I will point out that if you have a cell in which the used enters mL of phosphoric acid and another cell where that is multiplied by density and multiplied by molecular weight and strength and another cell with trial pH, that the cell which does the calculation can get the necessary charge info by reference to a cell on another sheet as easily as it can reference a cell on the same sheet. IOW you wouldn't have to reorganize the whole thing if you didn't want to.
Actually I think it's more important to just get the broad understanding of how the mEq balance comes together and what my spreadsheet does conceptually, rather than look at each step of the solution of a cubic equation.
It's your spreadsheet and your decisions. I only suggest these things because they are things that I have used and found helpful.







![Craft A Brew - Safale BE-256 Yeast - Fermentis - Belgian Ale Dry Yeast - For Belgian & Strong Ales - Ingredients for Home Brewing - Beer Making Supplies - [3 Pack]](https://m.media-amazon.com/images/I/51bcKEwQmWL._SL500_.jpg)