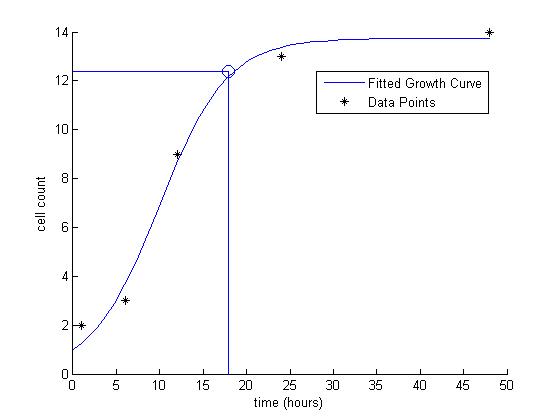
I’ve decided to look into the debate of using a starter or not. I, personally, do not usually use a starter very often, and have not noticed a difference. (Not to my eyes at least). But just because we can’t see it, doesn’t mean it’s not helping. Seeing as I love mathematics, I decided to let some famous dead mathematicians do some work for me. (I’m staring at you Liebniz and Newton).
The overall hypothesis is that the initial innoculation (starter size) has an impact on doubling time. And in fact, it does, as shown below.
Here’s what the plan is, if we can mathematically describe what is going on in a fermenter (according to the yeast population), maybe some interesting results will come about. The hardest part of this is translating a real system into mathematics, and then translating back to reality. But in between, since math follows a logic system (1+1=2 and so on…
we can manipulate the math anyway we please as long as the logic rules are not broken.
Maybe this is overkill, and you can just ask any seasoned brewer (not me… yet), and they will tell you how a starter is better or not. But I like my facts with a sweet side dish of math.
********************WARNING*********************
Plenty of math ahead. Not just adding and subtracting gravity readings, I'm talking calculus. So hold on to your pants, strap yourself in, and no refunds on the ride! WHEEE!
************************************************
We are going to start with the simplest idea possible. Yeast in a fermenter grow exponentially until saturation. Saturation is an iffy word and we need to clarify that. The basic idea is that the closer the yeast get to saturation, the slower and slower they grow. Now some naysayers will scream, “no wait!, my yeast grow faster and faster the longer they are in the fermenter!”. That is not the case- because if that did happen, the yeast would keep growing, blast out of the fermenter, and exponentially take over the world. Yikes. So all I’m saying is the yeast ‘start-off’ exponentially growing, then ‘slow-down’ until saturation.
I can now say that the growth of yeast is proportional to how much yeast there is. Think of it as this: if there is 1 yeast cell, after one division there will be 2. If there are 10 yeast cells, after one division for all cells (1 generation), there will be 20 cells. But it’s not that simple, yeast cells do not divide synchronously, and we have to factor in how long it takes them to divide. For those scienctists out there, this means that ‘continuous models’ are much better than ‘discrete models’. All right, so let’s write out what this proportionality means.
This ‘change in population over time’ is known in calculus as the ‘derivative of the population’. (Equivalently, think of velocity as being the derivative or change in position over some time.)
Proportionality basically means, “multiple of”. So we throw in a constant to get the following. Also note that ‘is’ means ‘equality’ in math.
“HOLD ON, what is r?” Good question. This ‘r’ value basically tells us how strong the proportionality is. We will call this ‘r’ value the ‘growth rate’. Just a definition. Well, this is almost where we want to be. If we ask a computer to graph this differential equation, we end up with exponential growth… at all times. If that was the case in reality, we would be covered in bacteria, and they would take over the universe.
Hmm… problem. Well we can safely say that they grow exponentially in the beginning, but the closer they come to this ‘saturation’, they slow down. This is where an idea called the ‘logistic equation’ comes along. Most people attribute this equation to the famous population geneticist, “Alfred Lotka” in the 1930’s, but it was actually derived 100 years earlier by a French Math guy, “Pierre Verhulst”.
Enough dabbling in history. What is this ‘logistic’? It is the idea that the population is self-limiting. The more population you have, the slower they grow. This population amount is measured relative to some maximum population that can exist. We will call this maximum population, K. So if the population of yeast ever does reach K, it will not grow at all. Drum roll please…
or
What? Well, it’s just an equation with two KEY properties, if P=K, then the logistic equation part is equal to zero, and if P is really close to zero, the logistic equation is really close to 1.
YAY! We have our equation. The most obvious question to ask (if you can follow my horrible explanation so far) is to ask how does the initial innoculum come into play?
The above equations are called “differential equations”. In order to solve these, you need a point on the graph, i.e., our initial innoculum. Here’s where the detials get messy, but as they say, you can’t have a good time until you get your feet wet.
******************Calculus-Haters skip the next section******************
We have
Here we will use the technique of solving called ‘separating of variables’. We will bring our P’s and t’s to separate sides and integrate.
We can’t quite integrate the left side yet, unless you can sporadically guess the solution, so we will use partial fractions to get,
Now we can integrate both sides directly (remembering our integrating constants),
Solving for P,
Solving for our integrating constant, we note that at t=0, P = (P_0), where (P_0) is our initial innoculum size.
And finally:
Please note that is is really hard to express an equation in a word document without some sort of equation editor.
***************************************************************
We are 95% done. All we have to know now is the doubling time. We have our final equation,
Where
P = Population size at a time t.
K = Saturation Limit.
P_0 = Initial population or Innoculum size. (Starter Size)
r = growth rate.
t = time.
To find the doubling time, set P = 2*P_0. I’m going to pull a fast one on you, and use the famous “It can be shown that”.
Ok the final punch line is this:
If I want to decrease my doubling time (DT), then I have to increase my starting population (starter size, P_0). If you can't see this, just convince yourself that the last term is an increasing function of P_0.
And there you have it. Either go through all the equations above, and verify my work, or go ask a brewer.
The overall hypothesis is that the initial innoculation (starter size) has an impact on doubling time. And in fact, it does, as shown below.
Here’s what the plan is, if we can mathematically describe what is going on in a fermenter (according to the yeast population), maybe some interesting results will come about. The hardest part of this is translating a real system into mathematics, and then translating back to reality. But in between, since math follows a logic system (1+1=2 and so on…
we can manipulate the math anyway we please as long as the logic rules are not broken.Maybe this is overkill, and you can just ask any seasoned brewer (not me… yet), and they will tell you how a starter is better or not. But I like my facts with a sweet side dish of math.
********************WARNING*********************
Plenty of math ahead. Not just adding and subtracting gravity readings, I'm talking calculus. So hold on to your pants, strap yourself in, and no refunds on the ride! WHEEE!
************************************************
We are going to start with the simplest idea possible. Yeast in a fermenter grow exponentially until saturation. Saturation is an iffy word and we need to clarify that. The basic idea is that the closer the yeast get to saturation, the slower and slower they grow. Now some naysayers will scream, “no wait!, my yeast grow faster and faster the longer they are in the fermenter!”. That is not the case- because if that did happen, the yeast would keep growing, blast out of the fermenter, and exponentially take over the world. Yikes. So all I’m saying is the yeast ‘start-off’ exponentially growing, then ‘slow-down’ until saturation.
I can now say that the growth of yeast is proportional to how much yeast there is. Think of it as this: if there is 1 yeast cell, after one division there will be 2. If there are 10 yeast cells, after one division for all cells (1 generation), there will be 20 cells. But it’s not that simple, yeast cells do not divide synchronously, and we have to factor in how long it takes them to divide. For those scienctists out there, this means that ‘continuous models’ are much better than ‘discrete models’. All right, so let’s write out what this proportionality means.
This ‘change in population over time’ is known in calculus as the ‘derivative of the population’. (Equivalently, think of velocity as being the derivative or change in position over some time.)
Proportionality basically means, “multiple of”. So we throw in a constant to get the following. Also note that ‘is’ means ‘equality’ in math.
“HOLD ON, what is r?” Good question. This ‘r’ value basically tells us how strong the proportionality is. We will call this ‘r’ value the ‘growth rate’. Just a definition. Well, this is almost where we want to be. If we ask a computer to graph this differential equation, we end up with exponential growth… at all times. If that was the case in reality, we would be covered in bacteria, and they would take over the universe.
Hmm… problem. Well we can safely say that they grow exponentially in the beginning, but the closer they come to this ‘saturation’, they slow down. This is where an idea called the ‘logistic equation’ comes along. Most people attribute this equation to the famous population geneticist, “Alfred Lotka” in the 1930’s, but it was actually derived 100 years earlier by a French Math guy, “Pierre Verhulst”.
Enough dabbling in history. What is this ‘logistic’? It is the idea that the population is self-limiting. The more population you have, the slower they grow. This population amount is measured relative to some maximum population that can exist. We will call this maximum population, K. So if the population of yeast ever does reach K, it will not grow at all. Drum roll please…
or
What? Well, it’s just an equation with two KEY properties, if P=K, then the logistic equation part is equal to zero, and if P is really close to zero, the logistic equation is really close to 1.
YAY! We have our equation. The most obvious question to ask (if you can follow my horrible explanation so far) is to ask how does the initial innoculum come into play?
The above equations are called “differential equations”. In order to solve these, you need a point on the graph, i.e., our initial innoculum. Here’s where the detials get messy, but as they say, you can’t have a good time until you get your feet wet.
******************Calculus-Haters skip the next section******************
We have
Here we will use the technique of solving called ‘separating of variables’. We will bring our P’s and t’s to separate sides and integrate.
We can’t quite integrate the left side yet, unless you can sporadically guess the solution, so we will use partial fractions to get,
Now we can integrate both sides directly (remembering our integrating constants),
Solving for P,
Solving for our integrating constant, we note that at t=0, P = (P_0), where (P_0) is our initial innoculum size.
And finally:
Please note that is is really hard to express an equation in a word document without some sort of equation editor.
***************************************************************
We are 95% done. All we have to know now is the doubling time. We have our final equation,
Where
P = Population size at a time t.
K = Saturation Limit.
P_0 = Initial population or Innoculum size. (Starter Size)
r = growth rate.
t = time.
To find the doubling time, set P = 2*P_0. I’m going to pull a fast one on you, and use the famous “It can be shown that”.
Ok the final punch line is this:
If I want to decrease my doubling time (DT), then I have to increase my starting population (starter size, P_0). If you can't see this, just convince yourself that the last term is an increasing function of P_0.
And there you have it. Either go through all the equations above, and verify my work, or go ask a brewer.
