Question about differences in calculated Mash pH shift due to mineralization

[Silver_Is_Money]

I've noticed that, with respect to Ca and/or Mg mineralization, mash pH programs (online and spreadsheet) that build upon the work of Kai Troester (Braukaiser) shift a mashes pH downward (from DI) by only at most about 60% vs. programs built along the lines of Bru'n Water.

This is a huge discrepancy, and primarily as a consequence of it the bottom line mash pH adjustment advice is radically different between the two approaches. Which approach is correct, or at least more so?

 

[ajdelange]

I don't know how either of those gentlemen approach it. I think the answer lies in Kolbach's observation that 1 mEq of alkalinity is cancelled by 3.5 mEq of calcium or 7 mEq of magnesium. Thus says that 3.5 mEq of calcium or 7 mEq of magnesium produces 1 mEq of protons and thus I simply tot up all the calcium and magnesium divided by 3.5 or 7 and add that many protons to the proton budget.

As Kolbach's observations pertain to knockout rather than the mash (I know Kai is aware if this and I am therefore pretty sure that this is why he reduces shift relative to the other programs) I often reduce the protons calculated as above by a factor of 0.7 or 0.5 before putting them into the budget used for mash pH prediction. I think we have to recognize that 3.5 mEq of calcium is an average as malts will contain more or less phytin bound in different ways and that, therefore, 3.5 is an approximation for a given malt. Fortunately, calcium and magnesium levels are generally modest and consequently the resulting pH shifts will be small so that the uncertainty is tolerable.

 

[Silver_Is_Money]

A.J.: So it appears that Kai's approach may be generally more true to the typical "real world" mash experience, or am I misunderstanding you here?

Given (for example) 5 Kg. of malts mashed in 20L of water, what downward pH shift should one realistically expect to witness when adding 4g of CaCl2 (or 4.7g of CaSO4) to either the strike water or the mash? Assume a DI mash pH of 5.50 for a grist aggregate totaling to 5 Kg.

 

[ajdelange]

4 g of CaCl2 is 4000/111 = 36 mmol containing 72 mEq of calcium. This would produce 72/3.5 = 20.57 mEq of protons to knockout. If there are 5 kg of malt with buffering of 50 mEq/kg•pH then the pH shift would be 20.57/(50*5) = 0.082 pH. In the mash we might expect to see half of the protons released in which case the shift would be 0.041.

 

[mabrungard]

Fortunately, my observations and experience differ from AJ's. For example, I just finished brewing a Dortmunder Export using a high chloride and sulfate content that is typical in the historic region. I used no acid in the mash and relied on the elevated calcium and magnesium content that I added to my RO water to bring the mash pH to my target of 5.31. The resulting final pH measured with my freshly calibrated Hanna Halo was 5.36. Curiously, the initial pH during the mash was 5.18 and it rose throughout the mashing duration, which is consistent with my contention that all mashes tend to have their pH move toward a pH of 5.4 (if your early pH is above 5.4, it tends to fall and it tends to rise if your initial pH is under 5.4).

I'm curious why someone makes an assertion that Kohlbach's widely recognized correlation with Ca and Mg content is in error when there is almost a hundred years of observations that support it? I do find consistently that it is still in effect and can and SHOULD be applied in making pH predictions.

 

[ajdelange]

Were Kolbach with us he would be the first to admit it is in error as pertains to mash as the paper containing the relevant observations were made on worts at knockout and pH reduction continues in the kettle if calcium is present. Clearly then the pH reduction will be somewhat less in the mash. Science does not yield nice round numbers like 3.5 and 7 so the 1 mEq of protons yielded by those amounts of, respectively, Ca and Mg is clearly an average as different malts are kilned in different ways and have different phytin contents. It is also clear that Kolbach's observations were made for the kind of beers found in the breweries he worked in which wouldn't include many northern brown ales. It is therefore completely reasonable to assume that there would be dispersion around the 1 mEq/L if one added 3.5 mEq of calcium to an ensemble of mashes made with various malts for beers not limited to German lagers. Thus one concludes that 3.5 and 7 are in error (they are averages and the real world puts dispersion about them) at knockout because of variability in malts and in the mash because the reaction isn't complete. Though none of the techniques of modern data collection and analysis are mentioned in Kolbach's paper I'm pretty sure he would be able to understand the science were it explained to him.

I assumed in my previous post and above that you are calculating proton surfeits from Kolbach's observations on alkalinity suppression but he also observed that knockout pH was suppressed 0.00168 pH for each ppm reduction in Residual Alkalinity. Should you be using that method to calculate pH reduction you add additional sources of error so that now you have
1)The erroneous assumption that 3.5 mEq Ca++ or 7.0 mEq Mg++ produce exactly 1 mEq protons in every mash
2)The erroneous assumption that the knockout result applies to mash
3)The erroneous assumption that all mashes/worts have the same buffering capacity.
4)The erroneous assumption that buffering is constant with pH (that the titration curves for malts are linear).[Edit]


As for your contention that all mashes tend to pH 5.4 this would suggest some sort of buffering, in the sense we mean when we speak of 'a buffer', that is a peak in the buffering capacity of the mash at a particular pH. There is no such 'peak' in malts and mashes. As you can readily verify by simple calculation when you mix several buffers the 'staircase' appearance of the titration curve of the individual acids with multiple pKs flattens and a smooth curve results. The first derivative of this curve (the buffering capacity) may have a broad maximum but hardly of the sort one associates with a calibration buffer, for example. The three malts I used as examples for Palmer's book peaked at
1)Pneumatic Pilsner malt: 6.1
2)CaraPils 80L: 5.8
3)Chocolate 600L: 5.1

Though it would be possible to get mash pH's down to 5 and below by using enough 80L (its pHDI = 4.8) there certainly no exceptional buffering at pH 5.4. Note that when two malts are mixed their buffering peaks, even though broad, will flatten even further.
Were I to erroneously assume that there was a preferred mash pH based on this assumed buffering and my experience I would guess it is closer to 5.5.

Finally, when you mix malts, measure pH and find an initial pH that is lower than the final pH you are either seeing the electrode response (I think the Halo's are really cool but their responses are slow) or early release of acid from the more acidic malts. This is especially the case where sauermalz is being used as the acid is on the surface and goes into solution very quickly. Whether acidic malts in general get their acid into solution more quickly that base malts I wouldn't venture to guess. Another possibility is that the mash was not mixed and the probe was in a part richer in the colored malt than the base malt. If the initially measured pH is < pHDI for the most acidic colored malt then the reading should be ignored as it is clearly erroneous. If the electrode is coming out of pH 4 buffer it may be simply a question of response time.

The fact that you get answers you like using an iffy algorithm only means that the algorithm works some times. The reason for the right answer is that one error source (e.g. using the knockout value which lowers the pH estimate) is offset by another error (e.g. over estimating the buffering capacity which raises the pH estimate).

All of this does not say that one shouldn't use Kolbach's observations to predict the effect of the calcium/phytin reaction but some common sense needs to be applied to the use. It's obvious that the predictions of magnitude drop need to be reduced because they are at knockout. But by how much? 0.5? 0.6? 0.7? Who knows? As to whether the calcium factor is 3.5 for pilsner malt ant 3.7 or 3.3 for ale malts, again who knows.

Hope the curiosity is satisfied.

 

[Silver_Is_Money]

I'm curious why someone makes an assertion that Kohlbach's widely recognized correlation with Ca and Mg content is in error when there is almost a hundred years of observations that support it? I do find consistently that it is still in effect and can and SHOULD be applied in making pH predictions.

Kai Troester did his own testing, and through direct experimentation and measurement he documented mineralization related pH shift results that are only about 55-60% of the full 100% Kolbach ideal. This is right in line with A.J.'s 0.5 (50%), 0.6 (60%), 0.7 (70%) estimate.

I believe that Kolbach did his legendary work in the 1950's. I believe that the pH meter was invented sometime around 1934. Kai's work was done circa 10 years ago.

 

[ajdelange]

Kolbach's original work was done before WWII but was lost during that conflict. He therefore restated the results of the earlier work in the Die Einfluss der Brauwaßers... (1953) paper that we all reference today.

 

[ajdelange]

A.J.: So it appears that Kai's approach may be generally more true to the typical "real world" mash experience, or am I misunderstanding you here?

I never really answered this question. Kai was the one that pointed out to me that all Kolbach's results were for knockout wort. I translated that paper but never noticed this - classic 'can't see the forest for the trees'. It is, as noted, therefore reasonable to expect that mash pH's are going to be less depressed by Ca++ and Mg++ than knockout wort pH's. But by how much? Kai's experiments determined that. Thus he is indeed being 'real world' in the sense that he determined by experiment the extent to which knockout predictions should be increased to make them applicable to mash.

 

[Silver_Is_Money]

I never really answered this question. Kai was the one that pointed out to me that all Kolbach's results were for knockout wort. I translated that paper but never noticed this - classic 'can't see the forest for the trees'. It is, as noted, therefore reasonable to expect that mash pH's are going to be less depressed by Ca++ and Mg++ than knockout wort pH's. But by how much? Kai's experiments determined that. Thus he is indeed being 'real world' in the sense that he determined by experiment the extent to which knockout predictions should be increased to make them applicable to mash.

I assume by "knockout" that you mean Kolbach added minerals, and then mashed, but only measured their pH shift effect at the end of boil and also post boil cooling , well down stream of the active mashing stage of the process. Would this be correct?

 

[ajdelange]

I think he prepared worts with waters of different alkalinities and different concentrations of calcium and magnesium and compared the pHs of the worts at knockout. 'Knockout' refers to the point at which the wooden peg closing the kettle outlet is knocked out with a mallet. IOW it means the end of the boil. If a water with alkalinity A and Ca++ concentration of X mEq/L produced a wort with the same pH as a wort made from water with alkalinity A + 1 (mEq/L) and Ca++ concentration X + 3.5 (mEq/L) then he could conclude (as he did) that 3.5 mEq Ca++ cancels 1 mEq alkalinity (though he worked in dH). He could also do a linear fit (though not as easily as we do it today) of pH against Alk - ([Ca++] + 0.5[Mg++])/3.5 (= RA, the residual alkalinity) and conclude that knockout pH decreases y pH units per unit of decrease in RA.

 

[mabrungard]

The knockout caveat is an interesting wrinkle. However, I'm still seeing that the acidification effect of Ca and Mg still follow a similar trend and magnitude.

AJ, what were the trials that you performed that led to your findings? I'm still curious how we are seeing things differently.

 

[ajdelange]

Martin,

I suggest you read the Kolbach paper (http://www.wetnewf.org/pdfs/Brewing_articles/KolbachPaper.pdf) again paying special attention to paragraphs like this one:

"From experience there are insufficient experimental results for us to be able to indicate to
at least some extent precisely how much the pH of the wort changes when the residual
alkalinity changes by a particular amount."

Indeed within the paper he makes the statements
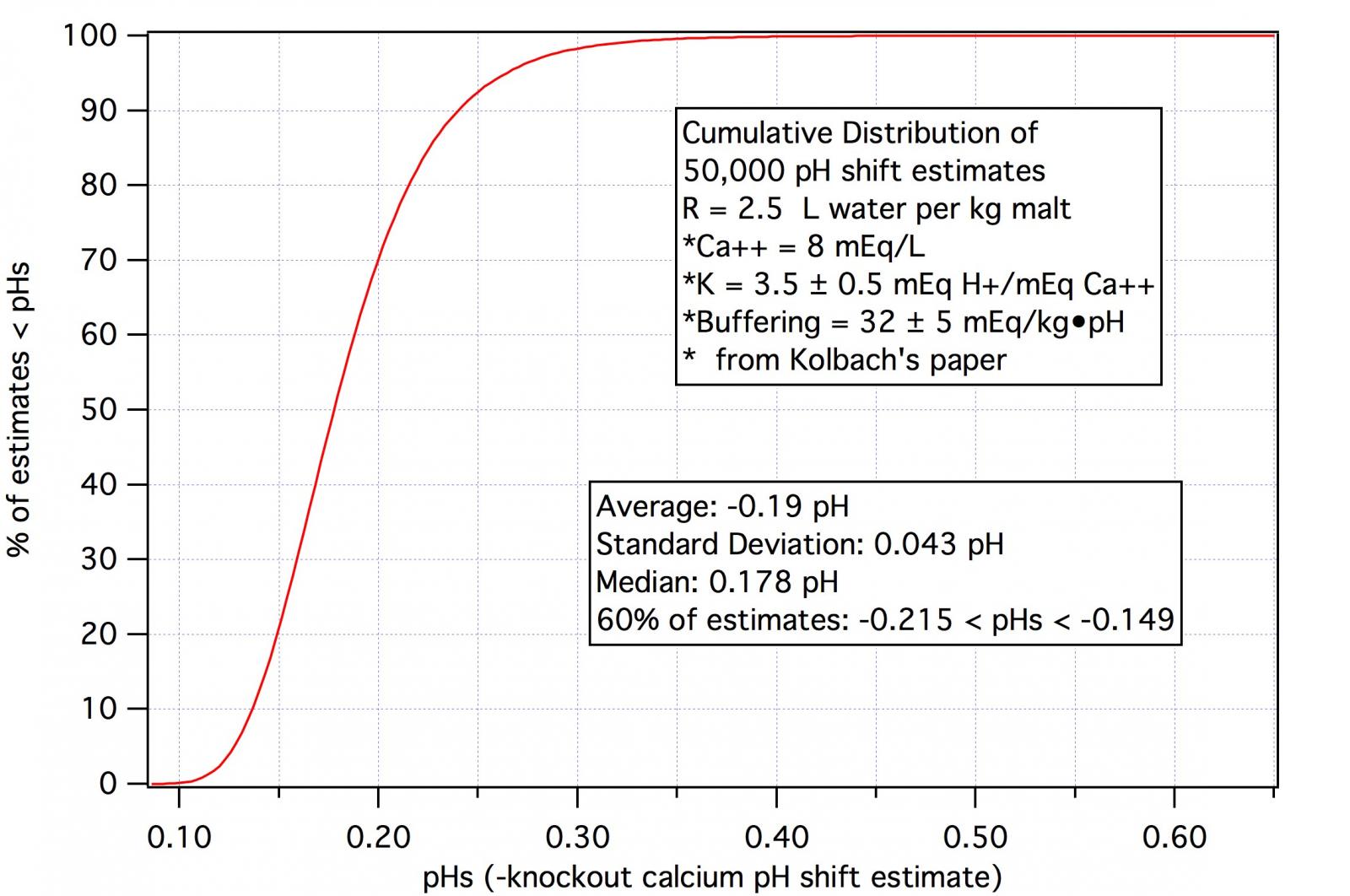
1) 3.5 mEq calcium offset 1 mEq alkalinity
2) A 10 ° dH (3.574 mEq/L) shifts the pH of a 12 °P beer by 0.3 pH
3) The buffering of wort is 32 mEq/ig&#8226;pH

Statements 1 and 3 imply a shift of 0.279 pH from a 10 ° RA shift which while not terribly different from 0.3 is different nevertheless. Furthermore, measurements on modern malts suggest that wort bufferings are going to be more like 50 mEq/kg&#8226;pH and, of course, will vary with the water to grist ratio i.e. the strength of the beer.

All of this suggests that there is going to be a fair amount of variability, on a percentage basis at least, in the pH shift per unit of RA shift over the range of typical brewing conditions. But the absolute values of shift are low. It is only in exceptional cases (and we note that Kolbach chose super hard Dortmund water for his examples) that the pH shifts are greater than 0.1.

I have not done any formal experimental evaluations of the shift in part because I know that the considerations mentioned above would mean that such a project would be no mean undertaking. If Kolbach couldn't do it I don't see how I could. I have, therefore, cleaved to the 3.5 mEq of calcium number and use that as the basis for all calculations. I think I have good estimates of malt buffering capacities so that part of my protocol is fairly robust but I am well aware that the actual number I would encounter with any real grist will not be 3.5 but only near it. Then there is the issue of knockout vs runoff wort. Even with all this uncertainty varying assumptions typically make differences in estimated pH shifts of a couple of hundredths. Even with the obscenely hard Dortmund water of Kolbach's paper (8 mEq/L or 400 ppm after decarbonation) the difference between 0.3 pH per 10 ° and using 3.5 mEq calcium to cancel 1 mEq of alkalinity with sound values for malt buffering the estimates are, respectively -0.2 pH and -0.1 pH at knockout and, presumably -0.1 and -0.5 in the mash tun. For more usual hardnesses the differences are a couple of hundredths.

 

[ajdelange]

It occurred to me that we might want to take a look at probable magnitudes in the variations of estimates of pH shift so that Martin, or anyone else who is interested, could get an idea as to how much in error an predicted pH shift might be. To begin we observe that the charge on the protons released by the calcium reaction is

Q = V*C/K

in which V is the volume of mash water in liters, C is the concentration of calcium ions in mEq/L and K is the Kolbach constant (nominally 3.5). The pH shift brought about by these protons is

dpH = Q/(m*B)

where m is the mass of the grains (kg) and B is the buffering in mEq/(kg&#8226;pH)

Thus dpH = V*C/(K*m*B)

But note that the volume of water is R*m i.e. some constant times the mass of the grains so

dPH = R*m*C/(K*m*B) = R*C/(K*B)

Now if we are uncertain as to the values of any of the factors in this formula we will be uncertain in dpH. The uncertainty, as a percentage of the number calculated by the formula will be sqrt(uR^2 + uC^2 + uK^2 + uB^2) where uK, for example, is the uncertainty is the Kolbach constant as a percentage of its value. For example, if we assume that the mean Kolbach constant is, as he has in his paper, 3.5 but think the standard deviation associated with that mean value is 0.5 then uK = 0.5/3.5 = 0.143 or 14.3%.

In the approach I take to calculating dpH I know how much water and grain I have and I calculate the buffering capacity of the grains from measurement data on malts which are as similar to the ones being used so that the only uncertainties I have are in K and in B. Assuming that the uncertainty in the Kolbach is indeed 14.3% and that the uncertainty in the buffering value is 15% (nominal buffering - and note that this should include the buffering attributable to any alkalinity is the water - is about 50 so we are guessing uncertainty of 7.5) we would then have

udPH = sqrt(14.3^2 + 15^2) = 20.7%

so that an estimated pH shift of 0.1 calculated by my method should be written as dpH = - 0.1 ± 0.02

So given these circumstances the error in the estimated pH shift would be but 0.02 which is small so it doesn't really matter, under these circumstances, that the error occurs. But what if the uncertainly in the Kolbach coefficient is 50% instead of 14%. That's a different story.

 

[ajdelange]

To gain further insight I calculated 50,000 calcium induced pH shifts using the parameters in Kolbach's paper for K (3.5), C (8 ,mEq/L) and B (32 mEq/kg&#8226;pH) with an uncertainty of 0.5 for K and 5 for B. The uncertainty was modeled by assuming that, for example, K is a Gaussian random variable with mean 3.5 and standard deviation 0.5. The plot below shows, on the y axis, the percentage of calculated estimates that were less, in magnitude, than the number on the x axis. Thus 50% of the calculation gave a pH shift magnitude less than 0.178 and 60% of them had magnitudes between 0.149 and 0.215.

 

[Silver_Is_Money]

Am I reading your chart properly, such that in a brewing environment (mash) with specific conditions present wherein Kolbach ideally predicts a downward mineralization pH shift of 0.30 points, in reality 70% of the time the real world pH shift witnessed will only be on the order of 0.20 pH points or less, and the percentage of mashes meeting the ideal Kolbach condition whereby the mash pH is actually moved downward by the anticipated 0.30 points will only occur at best a scant few percent of the time.

 

[ajdelange]

Not quite. It says that if you make a mash using 2.5 L of water containing 8 mEq/L Ca++ using malts such that the buffering of the grist is 32 mEq/kg&#8226;pH and put those numbers into the formula for pH shift using a value of 3.5 for the Kolbach constant you will calculate a pH shift of -0.19 pH (to knockout). But you don't know that the Kolbach constant is 3.5 nor do you know that your grist will have buffering of 32 mEq/kg&#8226;pH. If you assume the Kolbach constant to be a Gaussian random variable with mean 3.5 and standard deviation 0.5 and the buffering to be a Gaussian random variable with mean 32 and standard deviation 5 and generate numbers with those properties and stick them in the formula you will get answers which are distributed as shown by the curve. 10% of the answers will be less (in magnitude - these are all pH depression) than 0.14; 30% will be less than 0.16; half will be less than0.175 and nearly all will be less than 0.40. The average will be a depression of 0.19 pH.

If the uncertainties (standard deviations) in Kolbach constant and buffering are small relative to their means then the distribution of answers will be Gaussian and the standard deviation of 0.043 pH allows us to compute the relative frequencies easily by reference to a standard error curve. Even at the levels in this example the deviation from Gaussianity is noticeable but we can still use the standard deviation as a measure of the uncertainty in the prediction and assert that under these conditions the predicted knockout pH reduction is 0.19 ± 0.043.

 

[Silver_Is_Money]

Excellent! Thanks A.J.