Please advise on my tap water suitability for brewing.

[MajorJC]

Hey all,

I got my tap water tested by Ward Labs. Can I brew with it as is, or should I add something.

Thanks for the help.

Major

 

[Silver_Is_Money]

Looks like it's been ran through a water softener. Calcium, which is quite beneficial to brewing has been eliminated by the softener, and replaced with sodium, which is not so beneficial, and at 111 ppm sodium is way too high. And alkalinity is also way too high because water softeners do not eliminate alkalinity.

 

[MajorJC]

I don't have a water softener. It is supposed to be well water from my local water association. They wouldn't be using a water softener would they?

 

[Silver_Is_Money]

I don't have a water softener. It is supposed to be well water from my local water association. They wouldn't be using a water softener would they?

It certainly appears that way. The telltale signs of water softening are quite evident. Softeners eliminate calcium and magnesium (the cause of total hardness, which for your water is also zero) and replace them with sodium.

 

[Silver_Is_Money]

You can add calcium, but knocking down the sodium to a better level will require roughly 3 to 1 dilution with RO or distilled water, and after that you will still need to acidify the water to knock down or eliminate the alkalinity. If you have to go that far you might as well use straight RO water and add to it the minerals you desire. RO water has very little to no alkalinity, and also close to zero sodium.

My water softened well water is ballpark 250 ppm sodium and it's also loaded with alkalinity. I had an under the sink RO unit installed.

 

[mabrungard]

I don't have a water softener. It is supposed to be well water from my local water association. They wouldn't be using a water softener would they?

Yep, some do. However most wouldn't be softening to almost zero hardness like this sample shows. That is hell on your metal pipes.

My city partially softens the water supply via ion-exchange and aims for about 10 grains of hardness. That partially-softened water has less than 250 ppm sodium and it therefore does not taste salty.

 

[ScrewyBrewer]

So there’s no calcium no magnesium no total hardness but it has TDS of 259. So what dissolved solids are present in what otherwise could be RO water? Salt.

 

[Silver_Is_Money]

Total Dissolved Solids is in my opinion somewhat of a misnomer. TDS is merely another (and in my opinion, highly awkward) means of reporting a waters measured electrical conductivity. Generally (depending upon who made the specific TDS meter, and how they calibrated it, or what salt concentration and type they calibrated it with) TDS is virtually always found to be somewhere between 50% and 70% of the electrical conductivity of the water as reported in units of Microsiemens, or uS/cm. Notice that the OP's conductivity is actually reported as 0.43 mmho/cm. This is the equivalent of 430 Microsiemens of conductivity. (259/430)*100 = 60%. This means that Ward Labs particular TDS meter is calibrated to read out TDS in ppm as 60% of conductivity in Microsiemens.

You can look at a TDS meter as a meter that honestly internally measures Microsiemens, or uS/cm, and then multiplies it by a fixed internal fraction or percentage, and calls the result that appears on the screen TDS. Each manufacturer uses their own multiplier. I have a uS/cm meter by Hanna, and I emailed and asked them if I can also use it as a TDS meter, and they said "yes, and our chosen multiplier for TDS is 50% of uS/cm".

64% seems to be a quite common multiplier, but as I said, they are all over the board by manufacturer, but generally in my experience between 50% and 70% of uS/cm. And thus the awkwardness of TDS (at least as it relates to uS/cm).

 

[mabrungard]

Total Dissolved Solids is in my opinion somewhat of a misnomer. TDS is merely another (and in my opinion, highly awkward) means of reporting a waters measured electrical conductivity.

Uh, NO! Total Dissolved Solids is the sum of all ionic content in the water. However, I'll concede that the OP water report is an example of how the water's conductivity measurement is not an accurate estimate of TDS. Based on the reported ion concentrations, the actual TDS is closer to 380 mg/l and yet the value based on conductivity is reported as 259 ppm.

While TDS meters are useful tools, they aren't good at telling you how much (quantitative). However they are pretty good at telling you if its more or less than another sample (qualitative).

 

[Silver_Is_Money]

Martin, I was looking at TDS from the perspective of a TDS meter, which is how 99%+ of us would look at it. And is also likely how Ward Labs measures it.

The actual means to measure TDS is gravimetric, and it involves filtering a measured quantity of water, followed by weighing it, then evaporating it, and weighing it again. From this is derived TDS in ppm.

Per wikipedia, the two primary means of determining TDS are gravimetric (as above) and conductance. Of the two, gravimetric must be presumed to be far and away the most accurate, as conductance only appears to work highly accurately if the waters constituants are the same as the constituants of the TDS meters calibrant.

If one presumes that the Ward Labs TDS meter (which measures conductivity) is calibrated with a fixed quantity of pure NaCl or KCl (or other) in DI water (I.E., the calibrant solution), then simply by looking at the OP's water, one can see that it does not resemble DI water with NaCl or KCl (etc...) dissolved into it.

Since brewing source water (tap, well, or made up from RO, etc...) will never be a match for a TDS meters chosen calibrant, any given TDS meters value with regard to quantitative analysis is not high. It almost seems like a waste of effort for Ward Labs to provide this as part of their analysis, but perhaps it makes the end users feel better somehow.

 

[Silver_Is_Money]

Interestingly enough, if one is to sum the ionic constituents, one must sum only 50% of the HCO3- if expecting to achieve a degree of validity via this method.

https://www.usbr.gov/lc/phoenix/programs/cass/pdf/Phase1/ATechapdxTDS.pdf

Doing so for the OP's water we get:

TDS = 111 + 9 +8 + 4.8 + 246/2

TDS = 256

Rather close to 259... The difference likely being the 'minor' ionic components not represented on the Ward Labs report, plus those merely listed as <1 ppm.

I'm now willing to believe that this is how Ward Labs likely determines TDS, rather than via the use of a TDS meter.

If BW is predicting 380'ish ppm TDS, it simply needs to be corrected as to its reporting for TDS via dividing HCO3- by 2. The pdf linked above provides the reasoning behind this. In the end it will still remain merely an estimate, which is why Ward Labs indicates it as such. True TDS is to be derived via the gravimetric method.

 

[ScrewyBrewer]

@mabrungard and @Silver_Is_Money thank you for your deep dive into the world of total dissolved solids and TDS readings. I use the RO filter's TDS readings of the source and output water as an indicator for when the RO membrane needs replacement. This weekend I'll use my Hanna meter to compare its readings with the filter's readings.

 

[Silver_Is_Money]

@mabrungard and @Silver_Is_Money thank you for your deep dive into the world of total dissolved solids and TDS readings. I use the RO filter's TDS readings of the source and output water as an indicator for when the RO membrane needs replacement. This weekend I'll use my Hanna meter to compare its readings with the filter's readings.

Interestingly enough, when the HCO3-/2 correction is applied to summed ionic concentrations method of calculating TDS, my own TDS meter readings snap much closer in line with the summed ions TDS method, despite my well water having no resemblance to the calibrant for my meter.

 

[mabrungard]

I had not seen that correction before, but it makes sense if the evaporite analysis is to be used.

I know that the 'divide by 2' factor is close enough, but the true factor should actually be 60/122.

Looks like I'll be revising the TDS calculation in Bru'n Water.

 

[Silver_Is_Money]

I actually have both a budget TDS meter and a well more expensive uS/cm meter. On my well water, my TDS meter reads ~876, and my uS/cm meter reads ~1,280, and the ion summation model (with HCO3- correction applied) gives me 862.

1,280 x 50% = 640

But 1,280 x 64% = 819

Perhaps my Hanna Microseimens meter is better served for TDS purposes by applying the far more commonly seen 64% factor, despite what Hanna says. ????

 

[ajdelange]

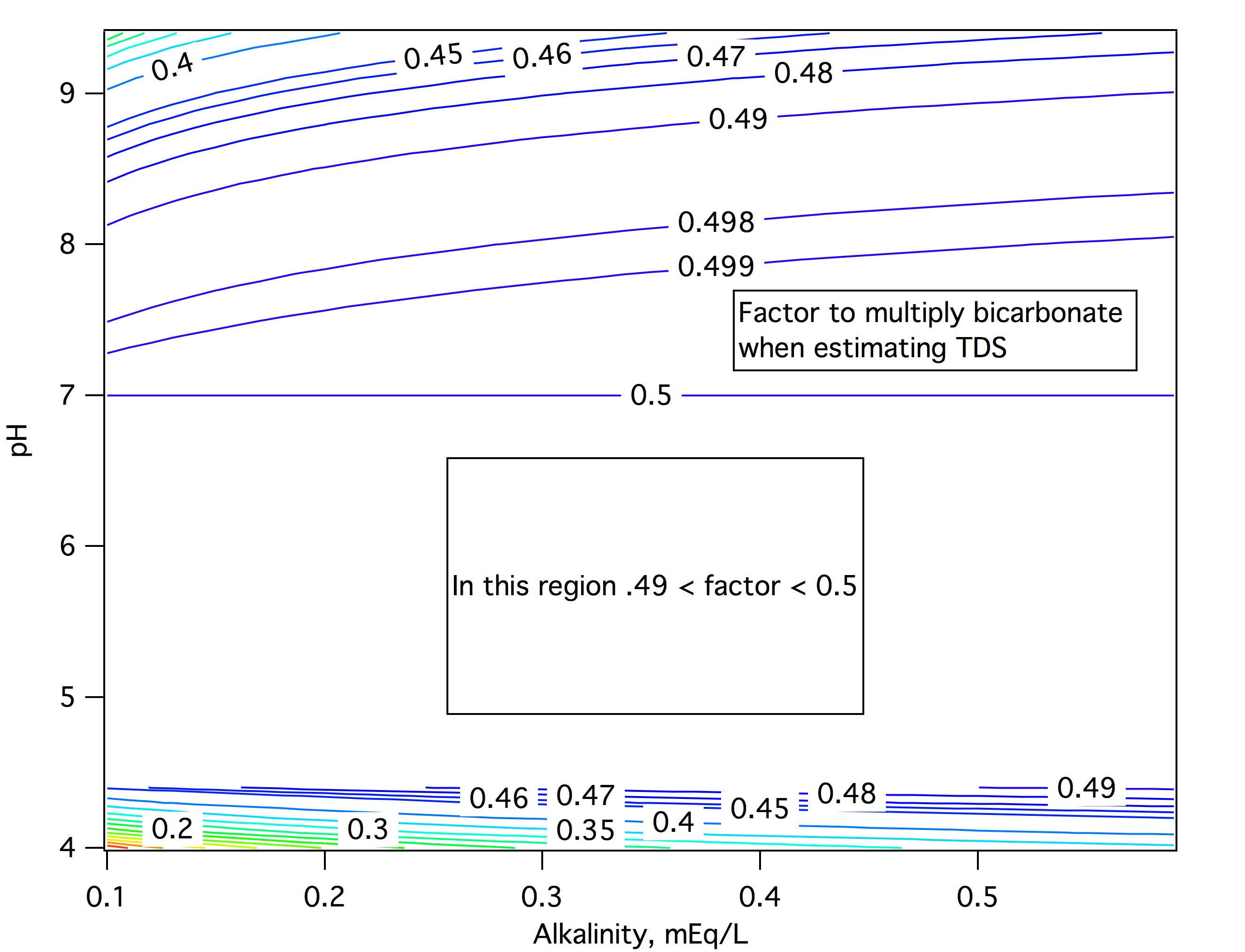
Interestingly enough, if one is to sum the ionic constituents, one must sum only 50% of the HCO3- if expecting to achieve a degree of validity via this method.

I had never thought of that nuance (always sloppily thinking of TDS as representing Total Dissolved Stuff) but indeed the statement is true.

[Edit]: What followed here was a graph showing how much carbon dioxide escapes when a calcium bicarbonate solution is evaporated as a fraction of the bicarbonate but that's not what we are talking about. We don't care about the dissolved CO2 that stays as a gas that leaves. We are concerned about the part that became bicarbonate. [End Edit]

Here's how it works (this is the Brewing Science Formum): x moles of calcium carbonate is dissolved by y moles of carbonic acid derived from y moles of carbon dioxide and y moles of water. The y moles of CO2 represent the Total Dissolved Gasses (TDG) which, of course, they really don't as we don't enter the masses of dissolved nitrogen, CO2, argon etc. In any case charges must balance. From x moles of CaCO3 we get 2*x positive charges from the calcium ions and x*Qc negative charges from the bicarbonate ions that are formed from the x moles of CaCO3. Qc is the charge on 1 mole of carbo, is a negative number and is a function of pH. The y moles of dissolved CO2 lend further negative charge of y*Qc. Thus 2*x + x*Qc + y*Qc = 0 as charge must balance.

The total carbo is Ct = x + y. Thus we have two equations we can easily solve for y, the amount of dissolved CO2:

y = Ct/( 1 - (Qc/(2 + Qc)))

[Edit] The part of y that leaves as dissolved but unconverted (to bicarbonate) is f0*Ct (fi is the fraction of Ct that carries charge -i) so the amount of CO2 leaving that comes from the bicarbonate is y - f0*Ct. The bicarbonate in the solution if f1*Ct so the fraction of this that goes out as CO2 is (y - f0)/f1.

For convenience set Ct = 1. Then y = 1/(1-Qc/(2+Qc)) = 1/(2/(2 + Qc) =1 - Q/2 = 1 - f1/2 - f2. Then y -f0 = 1 - f0 - f1/2 - f2. But f0 + f1 + f2 =1 implies that 1 - f0 - f2 = f1 so that y - f0 = f1 - f1/2 = f1/2 and dividing by f1 gives (y - f0)/f1 = 0.5. Exactly! The only thing we have neglected here is the charge on the water itself which will have an effect.

In the first equation we should have

2*x + x*Qc + y*Qc + Qw = 0 as charge must balance. The solution for y becomes

y = ( Ct + Qw/(2 + Q)) / ( 1 - (Qc/(2 + Qc))) and we can proceed as before except that it is clear that the effect of Qw is going to depend on the total carbo in the water. For large amounts of carbo it will dominate and the factor will be close to 0.5. For weaker (less alkaline) solutions the effect will be stronger at high pH. I'll look into this further and post more if this surmise leads to a significant result.

 

[Silver_Is_Money]

Scanned it but can't find the part where they talk about this. Could you post the page no.?

A.J., it's right on page A-1, roughly about 3/4 of the way down the page.

 

[ajdelange]

A.J., it's right on page A-1, roughly about 3/4 of the way down the page.

Yes. Sure is. Thanks.

The problem is with their statement: "...under the evaporation method, carbon dioxide (CO2) and water of hydration (H2O) which make up approximately one-half of the HCO3 would be driven off and not included in the residue." which simply isn't true at lower pH unless I screwed up and I think I did. I'll post when I get No. 16 right.

 

[RPh_Guy]

Interesting thread. Thanks brew science team!

I had an under the sink RO unit installed

Is this cost-effective? I buy RO water at 37 cents per gallon (US).

I probably use less than 80 gallons a year. That's $30.

 

[Silver_Is_Money]

Interesting thread. Thanks brew science team!


Is this cost-effective? I buy RO water at 37 cents per gallon (US).

I probably use less than 80 gallons a year. That's $30.

The closest RO water to me is a 13 mile round trip, so I have to factor in the cost of the water, plus fuel and wear and tear on our vehicles. The rock bottom budget RO unit we had installed cost only about $140 on a close-out. I can't remember what the install charge was. We found (when drinking and cooking with bottled RO water) that we typically used about 2 gallons per average day. Our cost is $0.30/gallon for bottle refill RO water, or about $220 per year.

The budget unit we had installed knocks our ~860 ppm TDS well water down to ~45 ppm TDS. I'm certain that there are better units.

 

[Silver_Is_Money]

An aside here (warning, loose ballpark rule of thumb time. A.J., sit down and take a deep breath please). If you have an RO unit, and you know your post RO unit ppm as TDS, you can ballpark your RO waters ppm alkalinity at roughly about 85% of TDS. Don't use this ballpark for anything other than RO water.

Disclaimer: Not a lot of thought or science went into this....

 

[ajdelange]

OK - No. 16 is fixed. I was answering the wrong question.

 

[MajorJC]

Ok, I zoned out on most of the discussion on this. Am I to understand that my best option is to buy the gallons of distilled water at Kroger, I don't know if I have a local source to buy RO water, and add stuff to it? If so, what should I be adding?

 

[Horseflesh]

Well, what you add depends on the beer you want to make.

You may need to add acid when making light beers, to get mash pH in the right range. You may want to add minerals like chloride and sulfate for flavor. There should be a sticky in this forum with the basics.

 

[ajdelange]

Just to follow up on the tail end of No. 16 the graph below shows the dependence upon pH and alkalinity of the factor by which the bicarbonate ion mass should be multiplied when adding it onto the sum of the other ion's masses in order to estimate TDS more accurately.

This is one of those annoying situations where, while the statement "The factor is 0.5" (curious as to where Martin got 60/122) is incorrect it is only so at combinations of pH and alkalinity seldom encountered. So indeed the statement "...under the evaporation method, carbon dioxide (CO2) and water of hydration (H2O) which make up approximately one-half of the HCO3 would be driven off and not included in the residue." isn't true (depending, I suppose, on how you want to define "approximately") at the extremes of pH where the charge on the water molecules themselves begins to rival that on the bicarbonate and carbonate ions which means that not only must the pH be distant from 7 but the alkalinity must be low which means the bicarbonate is going to be low. A Gen I spreadsheet probably does not need to incorporate this but a Gen II probably should as the math is simple (though it took me a while to figure it out).

 

[Silver_Is_Money]

Thanks A.J.! The deviation from 0.5 is overall far less than your initial post #16 had indicated. I'm happy with using 0.50.

 

[ajdelange]

Ok, I zoned out on most of the discussion on this.

That's likely to happen when you ask a question here. As this is the Brewing Science forum someone may respond to your question with some aspect of Brewing Science that isn't really what you are interested in.

Am I to understand that my best option is to buy the gallons of distilled water at Kroger,

There are three things going against you:
1) Your water is pretty high in alkalinity
2)The built in capability of your water to reduce that alkalinity, i.e. the calcium it used to contain probably at around 80 mg/L, has been removed
3)That calcium has been replaced with sodium

Thus this water is pretty much throw-away (though there are some things you could do with it) and for certain your path of least resistance is RO.

buy RO water, and add stuff to it? If so, what should I be adding?

That depends on what you want to brew. You can add whatever you want to it to get the qualities best suited for the beer you are brewing. When starting out you can do nothing more complicated than add half a tsp of calcium chloride plus half a tsp of calcium sulfate (if you like sulfate) to each 5 gallons. See the Primer in this forum.

 

[mabrungard]

(curious as to where Martin got 60/122)

I expect that you of all people would have been able to deduce that.

2HCO3 --> CO2 + H2O + CO3

The species of interest are HCO3 and CO3

HCO3 = 61 g/mol x 2 mol = 122g
CO3 = 60 g/mol x 1 mol = 60g

60/122 is plenty close enough to 0.5

 

[Silver_Is_Money]

60/122 = 0.4918, and that factor actually covers nigh on all generally encountered source water pH's rather well per A.J.'s chart. Seems even more practical for use than 0.5, but admittedly this is merely hair splitting.

 

[ajdelange]

I expect that you of all people would have been able to deduce that.

I was pretty sure what the numbers were but I was curious as to why you chose them to represent something approximately equal to 0.5 and why you called that the 'correct' answer when the 'correct' answer at pH 7 is 0.500000....

2HCO3- <--> CO2 + H2O + CO3--

This is the approximate equation and gives an answer which is approximately correct. The exact equation is

xCO3-- + yCO2 + yH2O <--> f0CO2 + f1HCO3- +f2CO3--

The f's are functions of pH equal to, respectively about 0.193407, 0.806256 and 0.000336104 at pH 7
Solving for x and y as I showed how to do earlier gives the ratio as 0.5 exactly at pH 7.