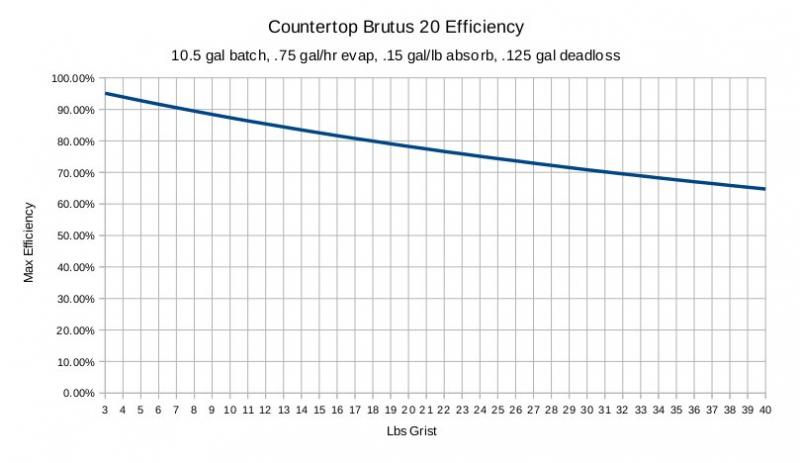
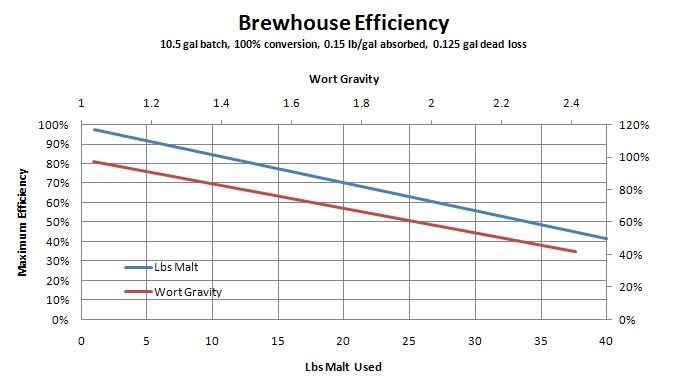
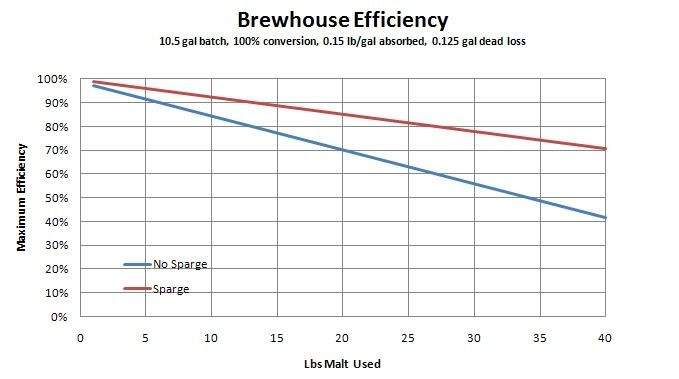
Now, to help you understand why boil time / evaporation is important, let's do the same example, adjusted for a 90 minute boil.
(Recall our original conditions: Say we want 5 gallons of 1.073 finished wort and want to do a 90 min boil. We know our system will boil off 0.75 gal/hr. Let's also assume our grist absorbs 0.125 gal/lb and our MLT has 0.25 gal of deadloss.)
Full Brutus 20 system volume will be 5 gal + (1.5 hr x .75 gal) + (12 lbs x .125 gal/lb) + .25 gal = 7.875 gal
444 / 7.875 = 56.4 points pre-boil
Now, back to your formula:
GRAIN = 12
PTS = 37
GRAVITY = 1.0564 (pre-boil; you said it doesn't matter)
VOLUME = 6.125 gal (again, pre-boil, per your requirement to be consistent)
"GRAVITY-1" = 56.4
56.4 * 6.125 = 345.45
12 * 37 = 444
345.45 / 444 = 77.8% efficiency.
So, simply by going from a 60 minute to 90 minute boil, NO other changes, our theoretical max Brutus 20 efficiency went up by a little over 1%.
OK OK, I think we're running in circles here. My issue wasn't your math, it was the statement that the boil directly affected your efficiency or the way your efficiency is calculated. To me it's not. It affects how much water you use, which then affects your efficiency (indirectly). I understand your point, but we're talking to different things (because we're looking at two different things). I calculate the amount of water I need seperately, thus the disconnect (a question of semantics).
People can get confused when you say that a longer boil will increase efficiency because they think "I'm increasing the gravity of my wort in the boil, thus increasing efficiency". This, of course, is not the case.
As for you last post, I'm not saying sugar as in "sucrose" or "table sugar". If we assume that wort is a mixture of only two things, water and sugar (of whatever kind), then every point of gravity above 1.0 is due to a sugar (of whatever kind).
0.31 lbs i the amount of sugar (of whatever kind) which should be produced from 1 lb of malt.
So, now that we're off of this tangent, let's go back to my original question. Your above comment that the gravity of the wort "lost" affects the overall efficiency (which I agree with completely) is of course the justification for using a sparge. The Brutus doesn't use a sparge, so the above logic means the efficiency must be lower. This means you need more grain to get the same amount of beer.
The Brutus also requires two pumps, so a higher cost to build (for me the pump was one of the largest expenses on my build).
It only uses two vessels, but if using tap water the system I drew in the first post only requires two vessels. Even if you're not using tapwater, you only need a small water bottle to hold the sparge water. (BTW, you can do the same cross circulation with the layout I've drawn).
So what I'm still not understanding, or seen shown, is what the advantage of the Brutus set up is? I'm not trying to knock it; it obviously works and is quite popular. However, the only advantage I see is the elmination of a small water bottle if not using tap water. If using tap water, I see no advantage at all?
Meanwhile there are multiple negatives, mainly a loss in efficiency and need for an additional pump?
So, again, what am I missing? Do the pros really outweight the cons, or are so many people building this system because it's been done before and is easy to duplicate?















































![Craft A Brew - Safale BE-256 Yeast - Fermentis - Belgian Ale Dry Yeast - For Belgian & Strong Ales - Ingredients for Home Brewing - Beer Making Supplies - [3 Pack]](https://m.media-amazon.com/images/I/51bcKEwQmWL._SL500_.jpg)