Ca(OH)2 and bicarbonate levels question

[Silver_Is_Money]

I've noticed that for both MpH and BW, an addition of calcium hydroxide leads to an increased level of bicarbonate. Since there is no bicarbonate ion associated with Ca(OH)2 is there a reaction mechanism taking place whereby bicarbonate is produced via the introduction of calcium hydroxide into mash water?

 

[mabrungard]

Of course not. However in the case of strong acids, 1 mole of OH neutralizes a mole of H. One mole of bicarbonate does the same.

 

[Silver_Is_Money]

Leaving aside its ability to neutralize hydronium ions, which is a given that is unquestioned as well as clearly not being discussed here, would it be accurate to say that people attempting to duplicate water profiles containing bicarbonate via the addition of Ca(OH)2 are being mislead?

 

[ajdelange]

Of course they are but Martin does not see it this way. He has in his defense that we tend to express alkalinity "as CaCO3" which has confused many, many here. Rather than attempt to clear some of the confusion, Martin chooses to increase it but he is, of course, perfectly free to do that if he wants to. It just makes the job of getting people to understand brewing water chemistry more difficult.

 

[ajdelange]

Of course not. However in the case of strong acids, 1 mole of OH neutralizes a mole of H. One mole of bicarbonate does the same.

As discussed here many times before and as recently as a few days ago (https://www.homebrewtalk.com/forum/threads/how-to-dispose-of-a-bottle-of-lactic-acid-88.659049/) the amount of H+ neutralizes depends on the pH to which you neutralize. If neutralizing to pH 5.2, for example, 1 mol of bicarbonate absorbs 0.938 mol of H+ ions. To pH 5.4 it absorbs 0.905. To pH 5.6, 0.857. Thus if dealing with its power to absorb protons from dark malt in order to get pH up to the low end of the acceptable range, its alkalinity is approximately (6% error at 5.2) 1 mol/mol. With the popularity of the notion that dark beers should be brewed with higher mash pH that error grows to 14% at 5.6 if you assume 1 mol/mol. This has been discussed here before and Martin had indicated that this error had been corrected in his program. I'll leave it to him to let you all know whether that is indeed currently the case.

 

[Silver_Is_Money]

A.J., on strictly an empirical weight ratio basis, what quantity of Ca(OH)2 would be the mash pH raising equivalent of NaHCO3 for the individual cases of targeting 5.2, 5.4, and 5.6 pH in the mash?

In the past I have simply ballpark presumed this weight ratio at 0.6 to 1.0 for Ca(OH)2 vs. NaHCO3, but obviously this purely empirical kludge of mine is a gross oversimplification. I.E., in my grossly simplified ballpark world view, adding 1.2 grams of Ca(OH)2 where an addition of 2 grams of baking soda is calculated as being actually required in order to achieve a targeted mash pH should get one "reasonably ballpark" close to the same final mash pH endpoint.

I presume that as opposed to applying this empirical 0.6X ballpark adjustment factor there is a real method for honing in the "factor of ratio adjustment" between baking soda and calcium hydroxide which is rooted in science.

 

[ajdelange]

Go to https://www.homebrewtalk.com/forum/threads/calculating-bicarbonate-and-carbonate.473408/ and carry out Steps 3 to 8 at the top of that post using the target pH, i.e. the pH you wish to neutralize to for the value of pHs. The result is Q(pHs) < 0 which is the charge on 1 mmol of carbo at that pH. If you add a mmol of NaHCO3 to water/mash/beer or whatever the charge on the carbo (1 mmol) is -1 mmol because all the carbo is, clearly, bicarbonate. Thus in going from the salt to pHs the charge increased from -1 to Q(pHs), that is, it increased by Q(pHs) - (-1) = 1 + Q(pHs) and thus 1 + Q(pHs) mmol of H+ must have been absorbed. Each mmol Ca(OH)2, as long as pHs < 8, clearly absorbs 2 mmol of H+ ions. Thus the ratio, on a molar basis, is 2/(1+Q(pHs)).

 

[Silver_Is_Money]

Go to https://www.homebrewtalk.com/forum/threads/calculating-bicarbonate-and-carbonate.473408/ and carry out Steps 3 to 8 at the top of that post using the target pH, i.e. the pH you wish to neutralize to for the value of pHs. The result is Q(pHs) < 0 which is the charge on 1 mmol of carbo at that pH. If you add a mmol of NaHCO3 to water/mash/beer or whatever the charge on the carbo (1 mmol) is -1 mmol because all the carbo is, clearly, bicarbonate. Thus in going from the salt to pHs the charge increased from -1 to Q(pHs), that is, it increased by Q(pHs) - (-1) = 1 + Q(pHs) and thus 1 + Q(pHs) mmol of H+ must have been absorbed. Each mmol Ca(OH)2, as long as pHs < 8, clearly absorbs 2 mmol of H+ ions. Thus the ratio, on a molar basis, is 2/(1+Q(pHs)).

For the most typical values of Q(pHs) I get a ratio on a weight basis of ~0.588 to 1 presuming that I've spreadsheet modeled this correctly. But I have low confidence that I did it correctly.

 

[ajdelange]

The protons absorbed by mL grams of Ca(OH)2 (lime) is 2*(mL/wL) where wL is the gram molecular weight of lime. The protons absorbed by mB grams of sodium bicarbonate is (mB/wB)*(1 + Q(pH)) where wB is the gram molecular weight of sodium bicarbonate. Thus, for equal proton absorption

mL/mB = (wL/2*wB) * (1 + Q(pH))

so that (wL/2*wB) * (1 + Q(pH)) grams of lime are required to do what 1 gram of bicarbonate does at pH. At very low pH the bicarbonate is most effective. Each mol neutralizes 1 mol of protons and in so doing is converted to uncharged (Q = 0) carbonic acid so (wL/2*wB) = 0.44 grams of lime are equivalent to 1 gram of NaHCO3. At pH 5.4 Q = -0.094789287, the bicarbonate is less effective as a base and a gram of it is, thus, equivalent to only 0.399 grams of lime. At pH 5.6 1 gram of bicarb is equivalent to 0.378 grams of lime and at pH 5.2 to 0.414. Thus if a constant conversion factor is wanted I guess I'd use 0.4 grams of lime per gram of bicarbonate.

 

[Silver_Is_Money]

For reference purposes only:

In MpH the ratio seems to be on the order of about ballpark 0.667 to 1

In BW the ratio appears to be on the order of about ballpark 0.55 to 1

So if the real answer is 0.4 to 1 (on average) then the spreadsheets offering a choice between baking soda and calcium hydroxide seem to be fairly far off the mark.

Is calcium hydroxide hygroscopic, such that it is not typically found at a concentration of 100% Ca(OH)2?

 

[ajdelange]

I'm fully aware that no one understands the Q thing so lets look at it from the viewpoint expressed by Martin in #2 i.e. that a mol of bicarb neutralizes an equivalent of acid and that a mol of Ca(OH)2 neutralizes 2. Given that the molecular weights of the two are about the same it is thus going to take about half as much lime as NaHCO3. Noting that a mol of lime weighs about 7/8 of what a mol of NaHCO3 weighs we expect it would take about 0.5*7/8 = 0.4375 grams of lime to do what a gram of bicarb does. It's that simple. So neither 0.55 or 0.667 is a reasonable answer even if you don't understand Q.

It would, thus, appear that the guys that do these spreadsheets don't even understand molecular weight but I think it's probably not that but rather in the way they model the effect of proton deficit on the mash pH. IOW I expect you tweaked Ca(OH)2 and NaHCO3 to get the same pH shift and compared the amounts required for the same shift.

 

[Silver_Is_Money]

The 0.44 ratio value can be derived this way:

Ca(OH)2 + 2HCl = CaCl2 + 2H2O
74g = 1 mole of calcium hydroxide

2NaHCO3 + 2HCL = 2H2CO3 + 2NaCl
84g = 1 mole of baking soda
2 x 84g = 168g

74g/168g = 0.440

So clearly the answer is not 0.6, and nor is it 0.55 or 0.667

Edit: I was formulating and typing this while A.J. was entering his post above.

 

[Silver_Is_Money]

IOW I expect you tweaked Ca(OH)2 and NaHCO3 to get the same pH shift and compared the amounts required for the same shift.

Yes, this is what I did in each spreadsheet. And my initial guess of 0.6 as the weight ratio factor was merely a ballpark tweener derived as a rough average between these two spreadsheets differing weight ratios.

 

[ajdelange]

It's
Ca(OH)2 + 2HCL --> CaCl2 + 2H2O
and
2NaHCO3 + 2HCl --> 2CO2 + 2H2O

Written thus it makes it clearer that in both cases 1 mol of H+ is absorbed per mol of HCl supplied and that it takes twice as many mol of bicarbonate as of Ca(OH)2 to do that (and corrects the number of water molecules formed in the Ca(OH)2 case.

 

[Silver_Is_Money]

So if for strong acids the ratio is ~0.44 to 1, is the lower ratio (of ~0.4 to 1 as a ballpark average) due to baking soda being such a weak base with respect to calcium hydroxide being a much stronger base?

Short version: Baking soda simply does not fully dissociate.

 

[ajdelange]

I expect you tweaked Ca(OH)2 and NaHCO3 to get the same pH shift and compared the amounts required for the same shift.

Yes, this is what I did in each spreadsheet.

The authors of these two spreadsheets should be very concerned that their pH prediction algorithms give different answers when equivalent amounts of alkali are added depending on the source of the alkalinity. This is clear evidence that the algorithms are basically (no pun intended) flawed.

There is great value in what you did here in the sense that you have discovered a simple test by which one can evaluate the worth of any program a brewer may wish to evaluate. Simply do what you did and verify that the ratio is about 0.4. If it is substantially different from that, you've got a program with a bad pH prediction algorithm.

Guess I should add that this won't uncover all flaws in a pH prediction scheme but as you have found this problem in the first two programs you tested we might suspect it will be found in others.

 

[ajdelange]

So if for strong acids the ratio is ~0.44 to 1, is the lower ratio (of ~0.4 to 1 as a ballpark average) due to baking soda being such a weak base with respect to calcium hydroxide being a much stronger base?

We didn't say anything about strong acids. 0.440995112 is the limiting case for very low pH (which may, of course, have been brought about by the use of strong acid but not only strong acids can produce low pH).

Bicarbonate ion is amphoteric meaning that it can be acidic (gives up protons) or basic (absorbs protons) depending on pH. Carbonic acid has two pKs: pK1 = 6.38 and pK2 = 10.38. These are the acid pKs. The basic equivalents are pKb1 = 7.62 and pKb2 = 3.62. The pKb's of Ca(OH)2 are 1.37 and 2.43. Thus Ca(OH)2 is better able to absorb both a first and second proton than bicarbonate ion and is, thus, a stronger base.

Short version: Baking soda simply does not fully dissociate.

Sort of. With lime Ca(OH)2 --> Ca(OH)+ + (OH)- governed by pKb1 and then Ca(OH)+ --> Ca++ + (OH)- governed by pKb2 so there is dissociation there. But with bicarbonate we have

HCO3- + H2O --> H2CO3 + (OH)- so it's really the water that gets pulled apart and the alkalinity comes from association rather than dissociation. But the relevant effect is that bicarbonate does not fully react unless the pH is low. The general rule of thumb is 2 pH units away from the governing pK which, in this case, is 6.38. Thus we would consider bicarbonate to react completely at any pH below 4.38 at which pH it can absorb 0.99 mEq of protons per mmol (99% reacted).

 

[dmr]

'm fully aware that no one understands the Q thing so lets look at it from the viewpoint expressed by Martin in #2 i.e. that a mol of bicarb neutralizes an equivalent of acid and that a mol of Ca(OH)2 neutralizes 2. Given that the molecular weights of the two are about the same it is thus going to take about half as much lime as NaHCO3. Noting that a mol of lime weighs about 7/8 of what a mol of NaHCO3 weighs we expect it would take about 0.5*7/8 = 0.4375 grams of lime to do what a gram of bicarb does. It's that simple. So neither 0.55 or 0.667 is a reasonable answer even if you don't understand Q.

It would, thus, appear that the guys that do these spreadsheets don't even understand molecular weight but I think it's probably not that but rather in the way they model the effect of proton deficit on the mash pH. IOW I expect you tweaked Ca(OH)2 and NaHCO3 to get the same pH shift and compared the amounts required for the same shift.

The 0.44 ratio value can be derived this way:

Ca(OH)2 + 2HCl = CaCl2 + 2H2O
74g = 1 mole of calcium hydroxide

2NaHCO3 + 2HCL = 2H2CO3 + 2NaCl
84g = 1 mole of baking soda
2 x 84g = 168g

74g/168g = 0.440

So clearly the answer is not 0.6, and nor is it 0.55 or 0.667

Just found this thread. I checked my MpH calculator version 3.0 for the issue discussed here. Now this version does not account for the fact that HCO_3^- is not fully neutralized at typical mash pH values. However, it does calculate (essentially) equivalent normality values for (e.g.) 1.68 gm of NaHCO_3 and 0.74 gm of Ca(OH)_2, as it should.

I wrote this spreadsheet quite some time ago, and so I'd have to dig through my notes to really check all of its calculations. However, I'd be really surprised if any of the normality calculations are wrong in MpH as (IIRC) I was careful to check such calculations against KT's old Kaiser Water spreadsheet. Cheers!

P.S. This ain't multivariable calculus. Cheers, again!

 

[Silver_Is_Money]

I'm re-opening this thread. I now believe the difference between the calculated 0.44 grams of Ca(OH)2 as being the caustic equivalent of 1 gram of baking soda and the observed 0.55 to 0.667 grams to 1 for BW and MpH is due to the downward shift in mash pH that the calcium ion component of the Ca(OH)2 brings along with it. Thus the ratio of 1 to 0.44 between Baking Soda and Ca(OH)2 is skewed by the need to add more Ca(OH)2 just to counter the impact of its calcium component.

Short version: Two opposing pH phenomenon are going on at the same time with Ca(OH)2. The two hydroxyl groups (OH-) are raising the pH, while the calcium ion (Ca++) is reacting with malt phosphates and liberating H+ ions, acidifying the wort, and lowering the pH somewhat at the same time. I'm initially in agreement with ~0.55 grams of Ca(OH)2 as being roughly the pH reducing equivalent of 1 gram of baking soda within a typical mash.

 

[mabrungard]

I agree that AJ’s original assertion that baking soda does not dissociate and react does not agree with my observations. I find that BS does produce the degree of alkalinity that I originally assumed. But Larry’s contention that there is a counteracting affect from the phosphate precipitation is interesting. I’m not sure that it’s the reason there isn’t the difference above, but it could be an explanation.

 

[Silver_Is_Money]

I agree that AJ’s original assertion that baking soda does not dissociate and react does not agree with my observations. I find that BS does produce the degree of alkalinity that I originally assumed. But Larry’s contention that there is a counteracting affect from the phosphate precipitation is interesting. I’m not sure that it’s the reason there isn’t the difference above, but it could be an explanation.

I've also recently abandoned AJ's contention that Baking Soda does not fully react to completion due to dissociation issues. When CO2 is evolved (escapes) there is no longer a chance for the reaction to reverse (for that molecule of NaHCO3). With the evolution of CO2 for each successive molecule of NaHCO3, it seems that baking soda reactions in acidic environments should eventually drive to completion for baking soda. But then again, due to CO2 solubility, not all CO2 evolves as a gas, so some potential for reaction reversal must seemingly remain (albeit at a much reduced level than for the case where evolved CO2 is not considered). Hmmm???

The phosphate reaction that liberates H+ is associated with the calcium component of calcium hydroxide. This is not an issue that involves baking soda, as it has no calcium.

Edit: I believe that AJ also contends that there is a 6.90 pKa somehow associated with baking soda which causes it to act somewhat as an extremely weak acid and as a weak (yet far less weak by comparison) base at the same time. I figured that I'd just toss this into the mix of things to ponder.

 

[Silver_Is_Money]

One drawback of using calcium hydroxide in the mash may be that it isn't nearly as soluble in water as I had initially presumed. Its solubility drops rapidly as water temperature rises. At 65 degrees C. its maximum solubility is about 0.103 grams per liter. And at 70 degrees C. its solubility falls to 0.086 grams per liter.

 

[Silver_Is_Money]

It should be noted that even with this drawback calcium hydroxide is roughly 100 times more soluble in water than calcium carbonate.

 

[mabrungard]

One drawback of using calcium hydroxide in the mash may be that it isn't nearly as soluble in water as I had initially presumed. Its solubility drops rapidly as water temperature rises. At 65 degrees C. its maximum solubility is about 0.103 grams per liter. And at 70 degrees C. its solubility falls to 0.086 grams per liter.

Larry, at the concentrations that we might be needing in the mash, I don't think the reduction in solubility is really an issue. With that said, I still recommend that ALL minerals, bases, and acids be fully mixed into room temperature water before adding grains. That enables anyone to visually confirm that they are all dissolved.

 

[Silver_Is_Money]

This might be the method to determine a nominal equivalence of Ca(OH)2 to NaHCO3 with respect to raising mash pH .

MW of Ca(OH)2 = 74.09268, so therefore the Eq Wt of Ca(OH)2 = 37.0463
MW of NaHCO3 = 84.0066, so its Eq weight is also 84.0066

37.0463/84.0066 = 0.440993

If there was no calcium ion downward impact upon mash pH shift, then 0.440993 grams of Ca(OH)2 would be the alkalinity and thereby pH raising equivalent of 1 gram of baking soda.

But every mEq of added OH- brings along with it 1 mEq of Ca++

Per Kolbach it takes 3.5 mEq's of Ca++ to reduce 1 mEq of alkalinity.

1/3.5 = 0.2857 mEq of alkalinity reduction due to the calcium ion present within Ca(OH)2.

As a consequence of this, 0.2857 x initial Wt of Ca(OH)2 is required.

But then this corrective addition brings along with it 0.2857/3.5 = 0.08163 mEq's of alkalinity reduction, etc..., etc..., so on and so on, ad-infinitum.

This infinite chain can be represented mathematically as 1 + 0.2857 + 0.2857^2 + 0.2857^3 + 0.2857^4, + 0.3857^5 ... etc..., whereby 1 is the initial need for 0.440993 x baking soda, and the rest are needed additions of OH- mEq's to counter the calcium that comes with it each time, adding to infinity.

Solving for this gives:

1 + 0.2857 + 0.2857^2 + 0.2857^3 + 0.2857^4 + 0.2857^5 ... = ~1.39921 (plus a minuscule scooch more to account for the infinity part left off here)

So ultimately, to counter the pH reduction of its own calcium, and to bring equivalence to baking sodas pH rise in the mash, one must add:

0.440993 x 1.39921 = 0.617 grams of Ca(OH)2 for every calculated 1 gram of baking soda required (plus a minuscule scooch more). Call it ~0.618 grams.

So by solving an infinite equation the mash pH raising mEq equivalent of Ca(OH)2 to baking soda yields ~0.618 grams of Ca(OH)2 for every calculated gram of baking soda. Leaving aside their dissociation constant effects, ~0.618 grams of Ca(OH)2 should raise mash pH by the same amount as 1 gram of baking soda.

Is your mash pH assistant software in close agreement with this conclusion?

 

[ScrewyBrewer]

Larry according to the results of my testing using ezRecipe 3.01.04 you are correct in saying that .618 gram of Ca(OH)2 (slaked lime) is equal to 1.0 gram of NaHCO3 (baking soda). Starting out with the same water profile for testing and substituting only .618 a gram of Ca(OH)2 with 1.0 gram of NaHCO3. The estimated 5.27 pH value remained the same whether using either the .618 Ca(OH)2 or the 1.0 gram of NaHCO3 addition.

The use of slaked lime is shown in the top image and the use of baking soda in the bottom image.

.618 gram of Ca(OH)2 (slaked lime)

1.0 gram of NaHCO3 ( baking soda)

 

[Silver_Is_Money]

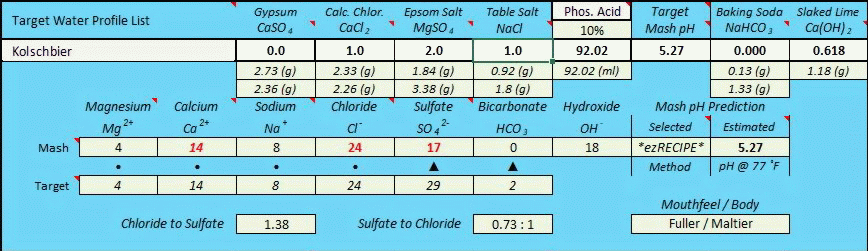
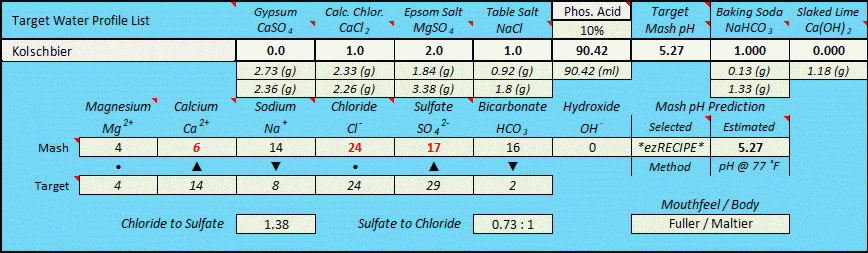
After having concluded the fixed 0.618:1 ratio (as per my infinite regression determination method seen above) I subsequently began to look at potentially critical pKa related ion dissociation factors, whereby baking soda is an extremely weak base with only partial dissociation at near mash pH due to its pKa1 value of 6.35 (which means that it is only 50% as basic at pH 6.35 as one would initially presume when using rudimentary level chemistry methods based solely upon stoichiometric equation balancing as I had initially been doing), and slaked lime is an extremely strong base with much higher levels of dissociation completeness at typical mash pH's, nearing complete dissociation, but not quite. If all else was equal between NaHCO3 and Ca(OH)2 the 0.618:1 ratio would clearly be true (and it may yet prove to work out to be that way), but in the real world all is likely not equal between them due to the vast differences in ion dissociation witnessed between them at typical mash pH's. Only actual "real world" 'side by side' testing of identical mashes utilizing both bases to raise pH will finally resolve this across the spectrum of pH's that are typically targeted, but for now I am cautiously presuming that it likely takes measurably less Ca(OH)2 than the "perfect world" work I did above would indicate, and that the equivalence ratio is highly pH target dependent and therefore not of a fixed value.

But it gets even more complex than settling upon a strictly pKa based solution, such as AJ deLange seems to lean toward in his math models (albeit that I do not want to, nor do I have any right to presume to speak for him, such that I'm not worthy to tie his shoes), since pKa related chemical equation reversal is clearly broken when one of the stoichiometry components of the "balanced" chemical equation evolves out of the solution mix (the developing wort in this case) as a gas, and is thereby no longer present in solution whereby to drive pKa associated equation reversal. For this case the breaks placed upon idealized reaction completeness via pKa related weak dissociation are somewhat lifted, and completion is more closely (and perhaps even fully) approached. But even gasses have solubilities and thereby do not completely evolve away....

I wish AJ was still actively participating on this forum, as his input would be much valued in assisting to resolve this. But the short answer is that the equivalency relationship of Ca(OH)2 to NaHCO3 is likely to be far more complex than an across the board presumption of either a fixed 0.618 to 1 ratio (due to the downward pH impact of the Ca++ ion within Ca(OH)2), or a 0.441 : 1 ratio based purely upon idealized stoichiomitry while ignoring any Ca++ impact, or a result based strictly upon dissociation constants (pKa or Ka), or a result based upon dissociation constants plus the Ca++ factor....

 

[ScrewyBrewer]

Still, I feel you've touched on an interesting concept, one providing just the kind of mind sport needed these days. As for AJ, I do wish him well. It seems he's taken down his website and has not replied to emails for some time now.

 

[Silver_Is_Money]

It is rather ironic that the 0.618 factor essentially splits the output difference I initially noticed between mPh 3.0 and Bru'n Water.