So the 6.38 and 10.38 constants are the pk's of Carbonic Acid which I believe you mentioned in a PM is adjusted by a formula in the routine pKCarbonic.
For the moment I'll just say yes and would leave it at that had you not stumbled across the pKa = 3.6 thing which I'll get to in a minute. 6.38 and 10.38 represent the values at 20 °C. pKCarbonic calculates pK's at other temperatures.
So at pH 6.38 (not sure of temperature) the Carbonic Acid dissociates from one of its H+ ions to form bicarbonate and at pH 10.38 the bicarbonate dissociates another H+ ion to form carbonate.
Consider the general case of an acid with n protons bound to A: HnA. As pH increases protons are stripped from the acid one at a time. We have a set of reactions
HnA <--> H+ + Hn-1A-
Hn-1A- <--> H+ + Hn-2A--
Hn-3A-- <--> H+ + Hn-3A--
The double headed arrows symbolize the fact that while the molecules are releasing protons they are simultaneously taking them back up and so the fundamental question becomes "What is the ratio of the number of molecules that have lost the (for example) first proton to the number that have retained it. This is where the pK's come in. The pK is proportional to the energy it takes to pry the proton off its molecule.
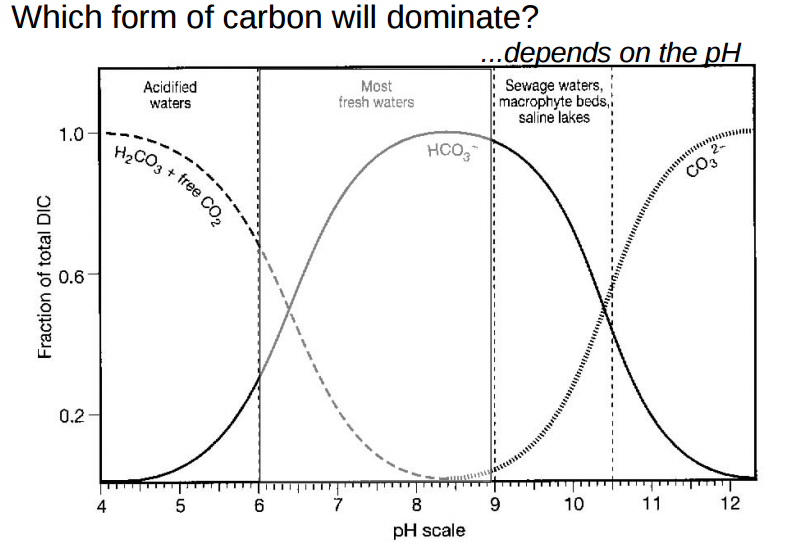
For the first proton we call the ratio [Hn-1A-]/[HnA] in which the bracketed terms represent the molar concentrations r1. It's value depends on the where the pH falls relative to the pK for that proton and has value r1 = 10^(pH - pK1). Thus when pH = pK1 the value of r1 is 1 and there are, thus equal numbers of molecules with all the protons and molecules that have lost the first one. Thus pK1 doesn't determine a threshold level at which the first proton is released but rather the level at which half of them have been released. Thus the curves for bicarbonate and carbonate cross in the picture in No. 6 at 10.38 - the second pK of carbonic acid. Half the bicarbonate ions have lost their (remaining) proton to become carbonate ions.
So what happens to those dissociated H+ ions? They are absorbed by the base that is added to raise the pH?
Take away the question marks. That is exactly what happens. But let's broaden that a bit and note that not only something added in order to increase mash pH absorbs protons (H+). Things that are already in the mash such as bicarbonate, carbonate, OH- and any malt whose DI pH is higher than the desired pH will absorb protons. The fundamental theorem of mash pH determination is that the quantity of protons emitted by acids (which are, by definition, things that emit protons) must be equal to the number of protons absorbed by bases (which are, by definition, substances which absorb protons). Protons are conserved. There are no electron capture decays going on in your mash tun. If there are get out of there tout suite!
Hrm... wikipedia mentions another pka of 3.6 so if we keep going left on the diagram what happens to the Carbonic Acid at that pka?
I'm really sorry you spotted this because dealing with it is likely to add confusion. I begged Palmer to keep this out of his book but he wouldn't. I was being disingenuous when I implied above that half of carbonic acid molecules have lost the first proton at pH 6.38. It is the fictitious species H2CO3* whose dissociation is half complete at pH = 6.38. When CO2 gas dissolves in water the CO2 molecules become entrained in a shell of water molecules. Only a small fraction of them actually react with the water to form carbonic acid. The molar concentration of H2CO3* is the sum of the molar concentrations of so-called aqueous (entrained) CO2 and the dissolved CO2 that actually reacted to form H2CO3. The reason we do this is that the equilibrium concentration of all the carbonic species of water under CO2 and over CaCO3 is determined by the partial pressure of the CO2. We multiply that partial pressure by the Henry coefficient to get [H2CO3*] and then calculate the concentration of bicarbonate [HCO3-] from r1 = 10^(pH - 6.38) in which 6.38 is the first pKa for H2CO3*. As you have probably guessed by now 3.6 is the pKa for real H2CO3. It is seldom that we care about the concentrations of true H2CO3 and CO2(aq) and so we usually use 6.38 and pretend that H2CO3* is really H2CO3. Now you will forever wonder when you see H2CO3 if the author is talking about H2CO3 or H2CO3*. If you don't see H2CO3* mentioned in an article and/or if the first pK is stated to be 6.38 then it is talking about H2CO3* even though it is writing it as H2CO3.
Pretty interesting stuff, I wonder if there are any textbooks with all of this stuff in or if it's just general chemistry knowledge.
The key to the whole thing is r = 10^(pH - pKa) and that is a direct consequence of the Henderson - Hasselbalch equation which in turn is the logarithmic form of the law of mass action as applied to the dissociation equation. So look for those two terms in indices and on the web.
You are definitely exploring the right part of the forest here. Grasp this and you will understand water and mash chemistry. Once the light comes on you will ask yourself why it seemed so hard when you started out.















![Craft A Brew - Safale S-04 Dry Yeast - Fermentis - English Ale Dry Yeast - For English and American Ales and Hard Apple Ciders - Ingredients for Home Brewing - Beer Making Supplies - [1 Pack]](https://m.media-amazon.com/images/I/41fVGNh6JfL._SL500_.jpg)










































